
19、(本小题满分14分)已知函数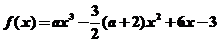 。
。
(1):当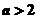 时,求函数
时,求函数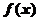 的极小值;
的极小值;
(2):试讨论函数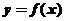 零点的个数。
零点的个数。
18、(本小题满分14分) 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,
垂足为A,PA=AB,点M在棱PD上,PB∥平面ACM。
(1):试确定点M的位置;
(2):计算直线PB与平面MAC的距离;
(3):设点E在棱PC上,当点E在何处时,使得AE⊥平面PBD?
17、(本小题满分12分)某机床厂每月生产某种精密数控机床10件,已知生产一件合格品能盈利8万元,生产一件次品将会亏损2万元。假设该精密数控机床任何两件之间合格与否相互没有影响。相关部门统计了近二年每个月生产的合格品,以生产最稳定的年份估算2010工厂生产该精密数控机床的合格率。
|
合格品 |
1月 |
2月 |
3月 |
4月 |
5月 |
6月 |
7月 |
8月 |
9月 |
10月 |
11月 |
12月 |
|
2008 |
7 |
8 |
7 |
6 |
10 |
8 |
5 |
6 |
7 |
8 |
6 |
6 |
|
2009 |
9 |
8 |
7 |
8 |
8 |
8 |
9 |
7 |
8 |
10 |
7 |
7 |
参考数据:
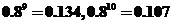
(1):试确定2010年生产精密数控机床的合格率;
(2):若该工厂希望每月盈利额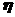 不低于70万元,求该工厂达到盈利目标的概率(将结果精确
不低于70万元,求该工厂达到盈利目标的概率(将结果精确
到0.01);
 (3):求该工厂每月盈利额
(3):求该工厂每月盈利额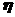 的数学期望。
的数学期望。
16.(本小题满分12分)已知向量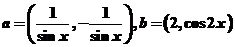 ,其中
,其中 .
.
(1)试判断向量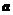 与
与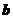 能否平行,并说明理由?
能否平行,并说明理由?
(2)求函数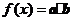 的最小值.
的最小值.
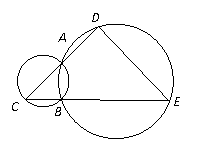
15. (几何证明选讲选做题)如图,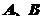 是两圆的交点,
是两圆的交点,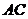 是小圆的直径,
是小圆的直径,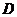 和
和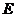 分别是
分别是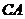 和
和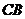 的延长线与大圆的交点,已知
的延长线与大圆的交点,已知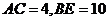 ,且
,且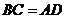 ,则
,则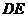 =___________.
=___________.
14. (坐标系与参数方程选做题)在直角坐标系中,曲线
(坐标系与参数方程选做题)在直角坐标系中,曲线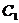 的参数方程为
的参数方程为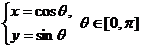 ,以
,以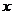 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线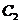 在极坐标系中的方程为
在极坐标系中的方程为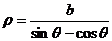 .若曲线
.若曲线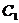 与
与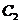 有两个不同的交点,则实数
有两个不同的交点,则实数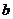 的取值范围是
.
的取值范围是
.
13.给出下列四个命题:
①命题
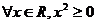 ,则
,则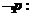
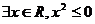 ;
;
②“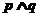 为真命题”是“
为真命题”是“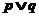 为真命题”
的充分非必要条件;
为真命题”
的充分非必要条件;
③若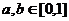 ,则不等式
,则不等式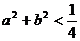 成立的概率是
成立的概率是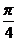 ;
;
④函数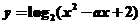 在
在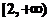 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是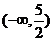 。
。
其中真命题的序号是 。(填上所有真命题的序号)
12、若与复数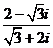 对应的向量为
对应的向量为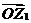 ,与复数1+
,与复数1+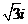 对应的向量为
对应的向量为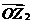 ,则
,则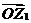 与
与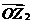 的
的
夹角等于___。
11.若点P为抛物线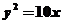 ,则点P到直线
,则点P到直线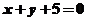 距离的最小值为___________。
距离的最小值为___________。
10.某企业三月中旬生产,A.B.C三种产品共3000件,根据分层抽样的结果;企业统计员制作了如下的统计表格:由于不小心,表格中A.C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是____________件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com