
23.(11分)已知抛物线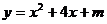 (m为常数)经过点(0,4)
(m为常数)经过点(0,4)
⑴求m的值;
⑵将该抛物线先向右、再向下平移得到另一条抛物线。已知这条平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为l1)关于y轴对称;它所对应的函数的最小值为-8.
①试求平移后的抛物线所对应的函数关系式;
②试问在平移后的抛物线上是否存在着点P,使得以3为半径的⊙P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被⊙P所截得的弦AB的长度;若不存在,请说明理由。
22.(10分)市园林处为了对一段公路进行绿化,计划购买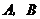 两种风景树共900棵.
两种风景树共900棵.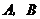 两种树的相关信息如下表:
两种树的相关信息如下表:
 项目 项目品种 |
单价(元/棵) |
成活率 |
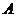 |
80 |
92% |
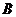 |
100 |
98% |
若购买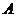 种树
种树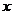 棵,购树所需的总费用为
棵,购树所需的总费用为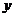 元.
元.
(1)求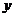 与
与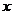 之间的函数关系式;
之间的函数关系式;
(2)若购树的总费用82000元,则购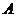 种树不少于多少棵?
种树不少于多少棵?
(3)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购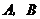 两种树各多少棵?此时最低费用为多少?
两种树各多少棵?此时最低费用为多少?
21.(10分)图1是小明在健身器材上进行仰卧起坐锻炼时情景.
图2是小明锻炼时上半身由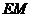 位置运动到与地面垂直的
位置运动到与地面垂直的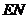 位置时的示意图.
位置时的示意图.
已知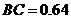 米,
米,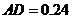 米,
米,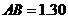 米.
米.
(1)求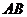 的倾斜角
的倾斜角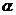 的度数(精确到
的度数(精确到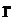 );
);
(2)若测得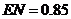 米,试计算小明头顶由
米,试计算小明头顶由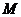 点运动到
点运动到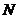 点的路径
点的路径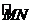 的长度(精确到0.01米)
的长度(精确到0.01米)


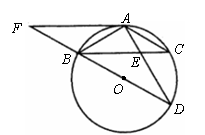
20.(9分)如图,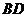 为
为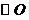 的直径,
的直径,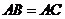 ,
,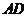 交
交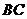 于
于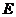 ,
, ,
,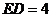 .
.
(1)求证: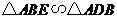 ,并求
,并求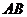 的长;
的长;
(2)延长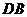 到
到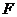 ,使
,使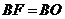 ,连接
,连接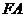 ,那么直线
,那么直线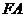 与
与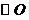 相切吗?为什么?
相切吗?为什么?
19.(9分)小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如右图:求一个回合能确定两人先下棋的概率.

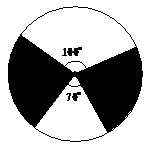
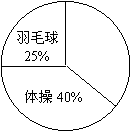
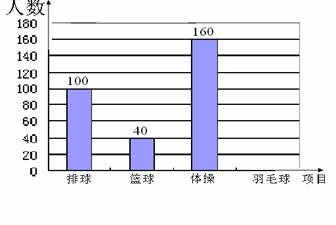
18.(9分)某学校为了学生的身体健康,每天开展
体育活动一小时,开设排球、篮球、羽毛球、体操课.学生
可根据自己的爱好任选其中一项,老师根据学生报名情况进
行了统计,并绘制了右边尚未完成的扇形统计图和频数分布
直方图,请你结合图中的信息,解答下列问题:
(1)该校学生报名总人数有多少人?
(2)从表中可知选羽毛球的学生有多少人?选排球和篮球的人数分别占报名总人数的百分之几?
(3)将两个统计图补充完整.
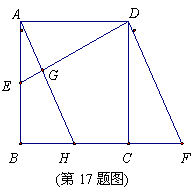
17.(9分)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(1)若把 绕点
绕点 旋转一定的角度时,能否与
旋转一定的角度时,能否与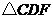 重合?请说明理由.
重合?请说明理由.
(2)现把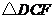 向左平移,使
向左平移,使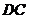 与
与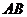 重合,得
重合,得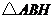 ,
,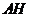 交
交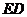 于点
于点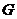 .
.
 求证:
求证: ,并求
,并求 的长.
的长.
16.(8分) 解方程: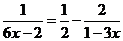






湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com