
49、如图所示,粒子源S可以不断地产生质量为m、电荷量为+q的粒子(重力不计).粒子从O1孔漂进(初速不计)一个水平方向的加速电场,再经小孔O2进入相互正交的匀强电场和匀强磁场区域,电场强度大小为E,磁感应强度大小为B1,方向如图.虚线PQ、MN之间存在着水平向右的匀强磁场,磁感应强度大小为B2(图中未画出).有一块折成直角的硬质塑料板abc(不带电,宽度很窄,厚度不计)放置在PQ、MN之间(截面图如图),a、c两点恰在分别位于PQ、MN上,ab=bc=L,α= 45°.现使粒子能沿图中虚线O2O3进入PQ、MN之间的区域.
(1) 求加速电压U1.
(2)假设粒子与硬质塑料板相碰后,速度大小不变,方向变化遵守光的反射定律.粒子在PQ、MN之间的区域中运动的时间和路程分别是多少?


解:(1)粒子源发出的粒子,进入加速电场被加速,速度为v0,根据能的转化和守恒定律得: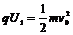 (2分)
(2分)
要使粒子能沿图中虚线O2O3进入PQ、MN之间的区域,
则粒子所受到向上的洛伦兹力与向下的电场力大小相等,
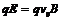
得到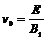 (2分)
(2分)
将②式代入①式,得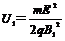 (1分)
(1分)
(2)粒子从O3以速度v0进入PQ、MN之间的区域,先做匀速直线运动,打到ab板上,以大 小为v0的速度垂直于磁场方向运动.粒子将以半径R在垂直于磁场的平面内作匀速圆周运动,转动一周后打到ab板的下部.由于不计板的厚度,所以质子从第一次打到ab板到第二次打到ab板后运动的时间为粒子在磁场运动一周的时间,即一个周期T.
小为v0的速度垂直于磁场方向运动.粒子将以半径R在垂直于磁场的平面内作匀速圆周运动,转动一周后打到ab板的下部.由于不计板的厚度,所以质子从第一次打到ab板到第二次打到ab板后运动的时间为粒子在磁场运动一周的时间,即一个周期T.
由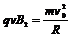 和运动学公式
和运动学公式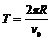 ,得
,得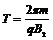 (2分)
(2分)
粒子在磁场中共碰到2块板,做圆周运动所需的时间为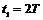 (2分)
(2分)
粒子进入磁场中,在v0方向的总位移s=2Lsin45°,时间为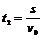 (2分)
(2分)
则t=t1+t2=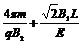 (2分)
(2分)
48、(南京市2008届第二次调研)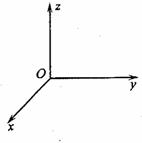 (本题12分)在同时存在匀强电场和匀强磁场的空间中取正交坐标系oxyz(z轴正方向竖直向上),如图所示。已知电场方向沿z正方向,场强大小为E,磁场方向沿y轴正方向,磁感应强度的大小为B,重力加速度为g。问:
(本题12分)在同时存在匀强电场和匀强磁场的空间中取正交坐标系oxyz(z轴正方向竖直向上),如图所示。已知电场方向沿z正方向,场强大小为E,磁场方向沿y轴正方向,磁感应强度的大小为B,重力加速度为g。问:
一质量为m、带电量为+q的从原点O出发的质点能否沿某一坐标轴上沿速度v做匀速运动?若能,m、q、E、B、v及g应满足怎样的关系?若不能,说明理由。


47、如图,真空中有一个平行板电容器,极板长L0=10cm,间距d=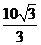 cm,两极板接在电压u=200sin(100πt )V的交流电源上,在平行板电容器右端L1=20cm处有一个范围足够大的匀强磁场,磁场方向垂直纸面向里,磁感应强度为B=
cm,两极板接在电压u=200sin(100πt )V的交流电源上,在平行板电容器右端L1=20cm处有一个范围足够大的匀强磁场,磁场方向垂直纸面向里,磁感应强度为B= ×10-2T.一束带正电的粒子以v0=
×10-2T.一束带正电的粒子以v0=  ×105m/s的速度沿着两极板的中轴线飞入电场,粒子的比荷q/m=1×108C/kg,不计粒子的重力.问:
×105m/s的速度沿着两极板的中轴线飞入电场,粒子的比荷q/m=1×108C/kg,不计粒子的重力.问:
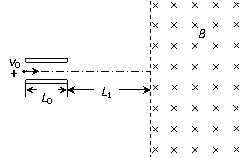 (1)何时飞入的粒子在电场中不发生偏转?这样的粒子进入磁场的深度多大?
(1)何时飞入的粒子在电场中不发生偏转?这样的粒子进入磁场的深度多大?
(2)何时飞入的粒子在离开电场时偏转最大?这样的粒子进入磁场的深度多大?
(3)第(2)问中的粒子从飞入电场到离开磁场经过的总时间为多大?
(1)粒子飞越电场的时间t0= L0/ v0 t0=( /3) ×10-6s (1分) T=0.02s t0<< T
/3) ×10-6s (1分) T=0.02s t0<< T
所以,每个粒子飞越电场的过程中,可以认为此时的电场是恒定的,要在电场中不偏转,条件是u=0 (1分) 即 100πt=nπ n=0、1、2、3…
100πt=nπ n=0、1、2、3…
所以进入的时刻为:t=n/100s (1分)
或 t1=0、10-2 s、2×10-2 s、3×10-2 s、4×10-2s...
在磁场中有B v0q=m v02/R R= m v0/Bq R=0.1m 即深度(1分)
(2)粒子飞越电场的最大偏转距离最多为d/2 假设这时的电压为U0
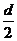 =
=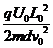 U0 =
U0 =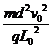 (1分) 代入得:U0=100V
(1分) 代入得:U0=100V
由100=200sin100пt
并考虑到对称性可得:t=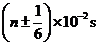 (2分)
(2分)
或 t2=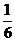 ×10-2
s、(1
×10-2
s、(1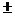
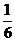 )×10-2 s、(2
)×10-2 s、(2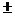
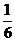 )×10-2 s、(3
)×10-2 s、(3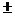
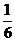 )×10-2 s、...
)×10-2 s、...
粒子的出射角度tan =
=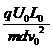 =
=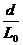 tan
tan =
=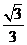
 =300(1分)
=300(1分)
出射速度v= 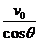 (1分)
R/ =
(1分)
R/ =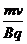 R/=
R/=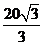 cm(1分)
cm(1分)
打入深度D= R/(1+sin ) (1分) D=10
) (1分) D=10 cm(1分)
cm(1分)
考虑到向上偏转的情况,打入深度D’= R’ (1-sin ) (1分)
) (1分)
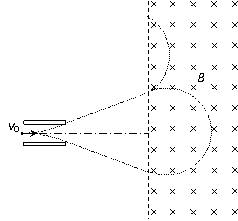 D’=
D’=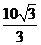 cm(1分)
cm(1分)
(3)在电场和磁场之间飞行时间t3=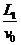 t3=
t3=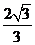 ×10-6s 在磁场
×10-6s 在磁场 中的飞行时间
中的飞行时间
t4=2T/3 T=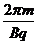 t4=
t4=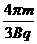
t总= t0+t3+t4= (1+
(1+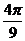 )×10-6s(1分)
)×10-6s(1分)
考虑到向上偏转的情况,在磁场中的飞行时间t5 =T/3
t’总= t0+t3+t5= (1+
(1+ )×10-6s (1分)
)×10-6s (1分)
46、如图所示,K与虚线MN之间是加速电场,虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行,电场和磁场的方向如图所示,图中A点与O点的连线垂直于荧光屏.一带正电的粒子从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U=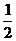 Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=
Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=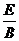 .若题中只有偏转电场的宽度d为已知量,则
.若题中只有偏转电场的宽度d为已知量,则
(1)画出带电粒子轨迹示意图;
(2)磁场的宽度L为多少?
(3)带电粒子在电场和磁场中垂直于v0方向的偏转距离分别是多少?
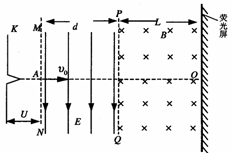
解:(1)轨迹如图所示
(2)粒子在加速电场中,由动能定理有
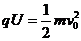
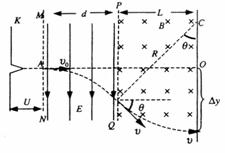 粒子在匀强电场中做类平抛运动,设偏转角为
粒子在匀强电场中做类平抛运动,设偏转角为 ,有
,有 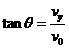
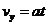
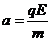
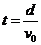
U=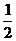 Ed
Ed
解得:θ=45º
由几何关系得,带电粒子离开偏转电场速度为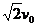
粒子在磁场中运动,由牛顿第二定律有:qvB=m[来源:学#科#网]
在磁场中偏转的半径为 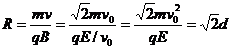
由图可知,磁场宽度L=Rsinθ=d
(3)由几何关系可得:带电粒子在偏转电场中距离为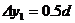 ,
,
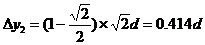
在磁场中偏转距离为
45、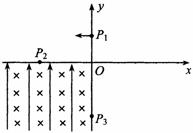 如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场。一质量为m、电荷量为q的带电质点,从y轴上y = h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x = – 2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y = –
2h处的P3点进入第四象限。已知重力加速度为g。求:
如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场。一质量为m、电荷量为q的带电质点,从y轴上y = h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x = – 2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y = –
2h处的P3点进入第四象限。已知重力加速度为g。求:
(1)质点到达P2点时速度的大小和方向;
(2)第三象限空间中电场强度和磁感应强度的大小;
(3)若在第四象限加一匀强电场,使质点做直线运 动,求此电场强度的最小值。
动,求此电场强度的最小值。
[解析](1)质点从P1到P2,由平抛运动规律
h
=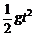 (1分)
(1分)
v0 =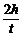 vy = gt (1分)
vy = gt (1分)
求出 v =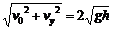 (1分)
(1分)
方向与x轴负方向成45°角 (1分)
(2)质点从P2到P3,重力与电场力平衡,洛仑兹力提供向心力
Eq = mg (1分)
Bqv = m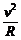 (1分)
(1分)
(2R)2 = (2h)2 + (2h)2
解得 E =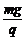 B
=
B
=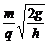 (2分)
(2分)
(3)质点进入第四象限做直线运动,当电场强度的方向与运动方向垂直时电场强度最小,由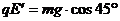 (2分)
(2分)
得: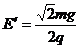 (2分)
(2分)
44、如图所示,MN是一固定在水平地面上足够长的绝缘平板(右侧有挡板),整个空间有平行于平板向左、场强为E的匀强电场,在板上C点的右侧有一个垂直于纸面向里、磁感应强度为B的匀强磁场,一个质量为m、带电量为-q的小物块,从C点由静止开始向右先做加速运动再做匀速运动.当物体碰到右端挡板后被弹回,若在碰撞瞬间撤去电场,小物块返回时在磁场中恰做匀速运动,已知平板NC部分的长度为L,物块与平板间的动摩擦因数为μ,求:
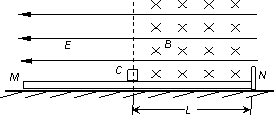 (1)小物块向右运动过程中克服摩擦力做的功;
(1)小物块向右运动过程中克服摩擦力做的功;
(2)小物块与右端挡板碰撞过程损失的机械能;
(3)最终小物块停在绝缘平板上的位置.
解:(1)设小物块向右匀速运动时的速度大小为v1,由平衡条件有
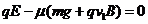 ①(1分)
①(1分)
设小物块在向右运动过程中克服摩擦力做的功为W,由动能定理有
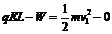 ②(2分)
②(2分)
由①②式解得
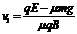 ③
③
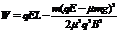 ④(2分)
④(2分)
(2)设小物块返回时在磁场中匀速运动的速度大小为v2,与右端挡板碰撞过程损失的机械能为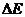 ,则有
,则有
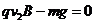 ⑤(2分)
⑤(2分)
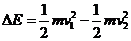 ⑥(1分)
⑥(1分)
由③⑤⑥式解得 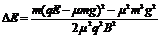 ⑦(2分)
⑦(2分)
(3)设最终小物块停止的位置在板上C点左侧x距离处,由能量守恒定律有
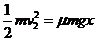 ⑧(2分)
⑧(2分)
由 ⑤⑧式解得
⑤⑧式解得 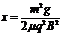 ⑨(2分)
⑨(2分)
43、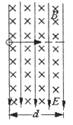 如图所示,某一真空区域内充满匀强电场和匀强磁场,此区域的宽度 d = 8 cm , 电场强度为E,方向竖直向下,磁感应强度为 B ,方向垂直纸面向里,一电子以一定的速度沿水平方向射入此区域.若电场与磁场共存,电子穿越此区域时恰好不发生偏转:若射入时撤去磁场,电子穿越电场区域时,沿电场反方向偏移量 y=3.2 cm :若射入时撤去电场,电子穿越磁场区域时也发生了偏转.不计重力作用,求: ( l )电子射入时的初速度的表达式; ( 2
)电子比荷的表达式: ( 3 )画出电子穿越磁场区域时(撤去电场时)的轨迹并标出射出磁场时的偏转角 α ; ( 4 )申子穿越磁场区域后(撤去电场时)的偏转角 α .
如图所示,某一真空区域内充满匀强电场和匀强磁场,此区域的宽度 d = 8 cm , 电场强度为E,方向竖直向下,磁感应强度为 B ,方向垂直纸面向里,一电子以一定的速度沿水平方向射入此区域.若电场与磁场共存,电子穿越此区域时恰好不发生偏转:若射入时撤去磁场,电子穿越电场区域时,沿电场反方向偏移量 y=3.2 cm :若射入时撤去电场,电子穿越磁场区域时也发生了偏转.不计重力作用,求: ( l )电子射入时的初速度的表达式; ( 2
)电子比荷的表达式: ( 3 )画出电子穿越磁场区域时(撤去电场时)的轨迹并标出射出磁场时的偏转角 α ; ( 4 )申子穿越磁场区域后(撤去电场时)的偏转角 α .
① v0=E/B
② q/m=2yE/B2d2
③ α=tan-12y/d
④ α=sin-12y/d
22.解:(1)设椭圆方程为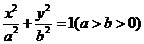
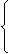
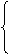 则
则 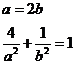 解得
解得 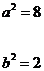
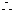 椭圆方程为
椭圆方程为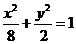 ………4分
………4分
(2) 直线
直线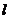 平行于
平行于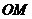 ,且在
,且在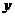 轴上的截距为
轴上的截距为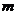 ,又
,又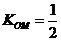
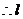 的方程为:
的方程为: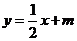 ………5分
………5分
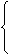 由
由 

 直线
直线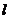 与椭圆交于
与椭圆交于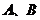 两个不同点,
两个不同点,
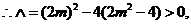
解得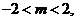 且
且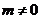 ………8分
………8分
(3)设直线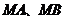 的斜率分别为
的斜率分别为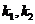 ,只需证明
,只需证明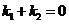 即可………9分
即可………9分
设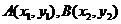 ,且
,且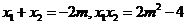
则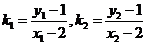
由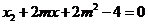 可得:
可得:
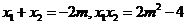
而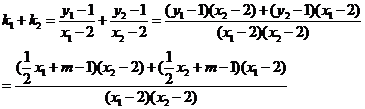 ………11分
………11分
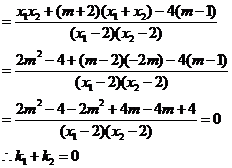
故直线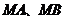 与
与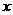 轴始终围成一个等腰三角形。………14分
轴始终围成一个等腰三角形。………14分
21.(本题满分12分)
(Ⅰ) 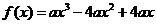
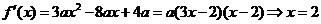 或
或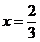 ………2分
………2分
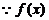 有极大值
有极大值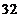 ,而
,而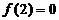 ………3分
………3分
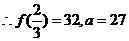 ………5分
………5分
(Ⅱ) 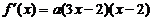
当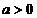 时,
时,
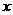 |
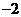 |
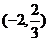 |
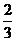 |
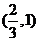 |
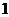 |
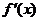 |
|
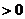 |
|
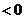 |
|
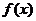 |
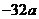 |
递增 |
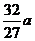 |
递减 |
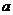 |
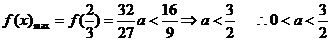 ………8分
………8分
当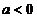 时,
时,
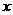 |
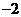 |
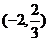 |
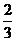 |
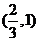 |
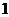 |
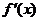 |
|
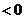 |
|
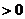 |
|
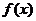 |
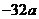 |
递减 |
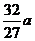 |
递增 |
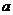 |
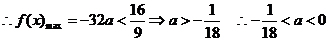 ………11分
………11分
综上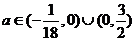 ………12分
………12分
20.解:(Ⅰ) 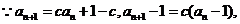 ……2分
……2分
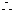 当
当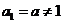 时,
时,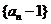 是首项为
是首项为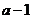 ,公比为
,公比为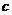 的等比数列
的等比数列
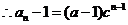 ,即
,即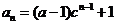 ……4分
……4分
当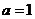 时,
时,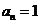 仍满足上式。
仍满足上式。
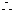 数列
数列 通项公式为
通项公式为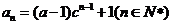 ……6分
……6分
(Ⅱ)由(Ⅰ)得,当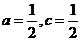 时,
时,
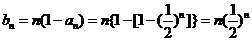 ……8分
……8分
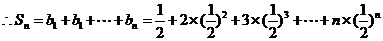
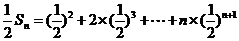
两式作差得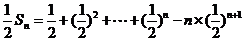
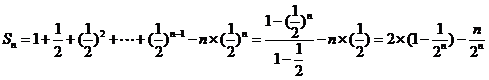
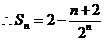 ……12分
……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com