
20.(本小题满分14分)
已知函数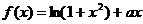 ,其中
,其中 为不大于零的常数.
为不大于零的常数.
(1) 讨论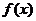 的单调性;
的单调性;
(2) 证明: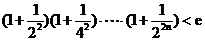 (
(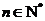 ,
,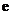 为自然对数的底数).
为自然对数的底数).
19.(本小题满分14分)
如图,在直角梯形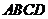 中,
中,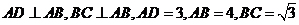 ,点
,点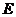 在线段
在线段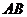 的延长线上.曲线段
的延长线上.曲线段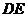 上任一点到
上任一点到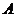 、
、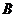 两点的距离之和都相等.
两点的距离之和都相等.
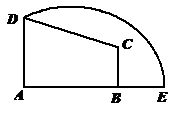 (1)建立适当的直角坐标系,求曲线段
(1)建立适当的直角坐标系,求曲线段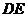 的方程;
的方程;
(2)试问:过点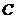 能否作一条直线
能否作一条直线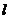 与曲线段
与曲线段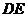 相交于两点
相交于两点
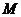 、
、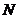 ,使得线段
,使得线段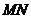 以C为中点?若能,则求直线
以C为中点?若能,则求直线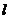 的方程;
的方程;
若不能,则说明理由.
18.(本小题满分14分)
如图,已知正方形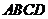 和矩形
和矩形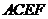 所在平面互相垂直,
所在平面互相垂直, 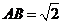 ,
,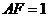 ,
,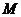 是线段
是线段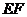 的中点.
的中点.
(1)求证: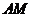 ∥平面
∥平面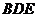 ;
;
(2)求二面角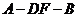 的大小;
的大小;
(3)试问:在线段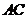 上是否存在一点
上是否存在一点 ,使得直线
,使得直线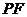 与
与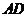 所成角为
所成角为 ?
?
17.(本小题满分12分)
某休闲会馆拟举行“五一”庆祝活动,每位来宾交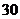 元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为
元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为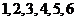 的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值之和为
的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值之和为 分,则获得价值为
分,则获得价值为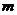 元的礼品;若抽得两球的分值之和为
元的礼品;若抽得两球的分值之和为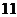 分或
分或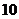 分,则获得价值为
分,则获得价值为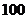 元的礼品;若抽得两球的分值之和低于
元的礼品;若抽得两球的分值之和低于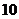 分,则不获奖.
分,则不获奖.
(1)求每位会员获奖的概率;
(2)假设这次活动会馆既不赔钱也不赚钱,则 应为多少元?
应为多少元?
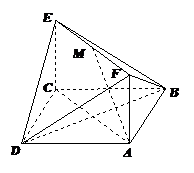
16.(本小题满分12分)
已知向量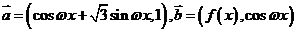 ,其中
,其中 >0,且
>0,且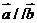 ,又函数
,又函数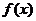 的图像两相邻对称轴之间的距离为
的图像两相邻对称轴之间的距离为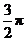 .
.
(1)求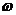 的值;
的值;
(2) 求函数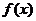 在区间
在区间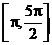 上的最大值与最小值及相应的
上的最大值与最小值及相应的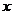 值.
值.
(一)必做题(9-13题.)
9. 一组数据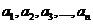 的方差为
的方差为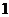 ,则数据
,则数据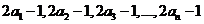 的方差为
的方差为
___________.
10.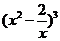 的展开式中的常数项为 .
的展开式中的常数项为 .
11. 已知曲线 在
在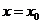 处的切线与曲线
处的切线与曲线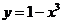 在
在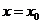 处的切线互相平行,则
处的切线互相平行,则
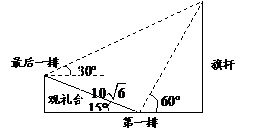
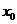 的值为
.
的值为
.
12. 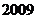 年北京国庆阅兵式上举行升旗仪式.如图,在
年北京国庆阅兵式上举行升旗仪式.如图,在
坡度为 的观礼台上,某一列座位与旗杆在同一个
的观礼台上,某一列座位与旗杆在同一个
垂直于地面的平面上,在该列的第一排和最后一排
测得旗杆顶端的仰角分别为 和
和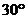 ,且第一排和
,且第一排和
最后一排的距离为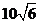 米,则旗杆的高度为 米. 第12题图
米,则旗杆的高度为 米. 第12题图
13. 若不等式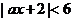 的解集为
的解集为 ,则实数
,则实数 的值为_____________.
的值为_____________.
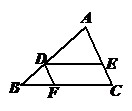 (二)选做题(14、15题,考生只能从中选做一题,两题都选的只计算第14题的得分.)
(二)选做题(14、15题,考生只能从中选做一题,两题都选的只计算第14题的得分.)
14. (几何证明选讲选做题) 如图,在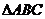 中,
中,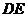 ∥
∥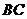 ,
,
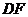 ∥
∥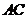 ,
,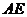 ︰
︰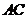 =
=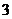 ︰
︰ ,
,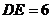 ,则
,则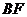 =____.
=____.
第14题图
15. (坐标系与参数方程选做题)若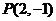 为曲线
为曲线 (
(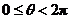 )的弦的中点,则该弦所在直线的普通方程为_____________.
)的弦的中点,则该弦所在直线的普通方程为_____________.
8.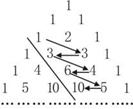 如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以
如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以
构成一个“锯齿形”的数列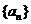 :
: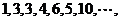 记其前
记其前
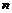 项和为
项和为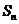 ,则
,则 的值为
的值为
A.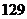 B.
B.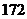 C.
C.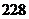 D.
D.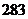 第8题图
第8题图
7. 下列三图中的多边形均为正多边形,M,N是所在边上的中点,双曲线均以图中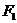 、
、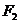 为
为
焦点,且三个图中的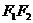 的长相等.设图①②③中双曲线的离心率分别为
的长相等.设图①②③中双曲线的离心率分别为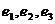 ,则
,则
A.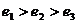 B.
B.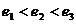 C.
C.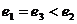 D.
D.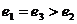
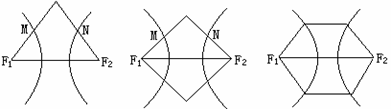
① ② ③
第7题图
6.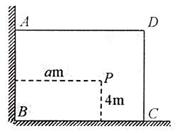 如图,有一直角墙角,两边的长度足够长,在P处有一棵
如图,有一直角墙角,两边的长度足够长,在P处有一棵
树与两墙的距离分别是 m
m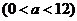 、
、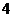 m,不考虑树
m,不考虑树
的粗细.现在想用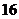 m长的篱笆,借助墙角围成一个矩形
m长的篱笆,借助墙角围成一个矩形
的花圃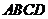 .设此矩形花圃的面积为
.设此矩形花圃的面积为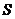
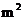 ,
,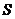 的最大
的最大
值为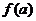 ,若将这棵树围在花圃内,则函数
,若将这棵树围在花圃内,则函数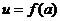 的
的
图象大致是
第6题图
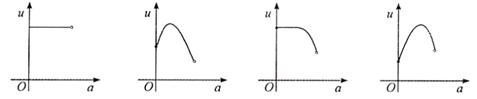
A. B. C. D.
5. 如图所示,在一个边长为1的正方形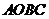 内,曲线
内,曲线
 和曲线
和曲线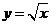 围成一个叶形图(阴影部分),
围成一个叶形图(阴影部分),
向正方形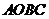 内随机投一点(该点落在正方形
内随机投一点(该点落在正方形
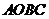 内任何一点是等可能的),则所投的点落在
内任何一点是等可能的),则所投的点落在
叶形图内部的概率是
A.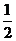 B.
B.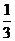 C.
C.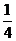 D.
D.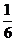 第5题图
第5题图
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com