
22. 解:(Ⅰ)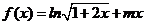 ,
,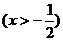 ∴
∴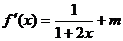
因为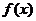 为定义域上的单调增函数
为定义域上的单调增函数
由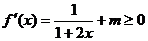 对
对 恒成立, ∴
恒成立, ∴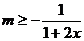 ,
,
而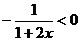 ,所以
,所以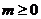
∴当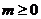 时,
时,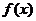 为定义域上的单调增函数
为定义域上的单调增函数
(Ⅱ)当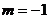 时,由
时,由 ,得
,得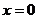
当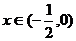 时,
时,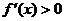 ,当
,当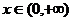 时,
时,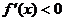
∴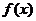 在
在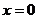 时取得最大值,∴此时函数
时取得最大值,∴此时函数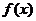 的最大值为
的最大值为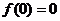
(Ⅲ)证法一:由(Ⅱ)得,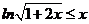 对
对 恒成立,当且仅当
恒成立,当且仅当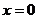 时取等号
时取等号
当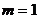 时,
时,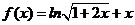 ,∵
,∵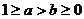 ,
,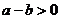
∴
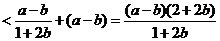 ∴
∴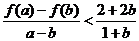
同理: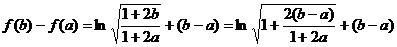
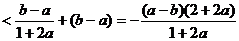
∴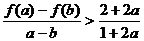
∵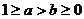 ,
,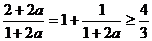 ,
, 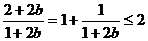
∴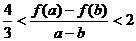
证法二:当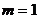 时(由待证命题的结构猜想,构造辅助函数,求差得之),
时(由待证命题的结构猜想,构造辅助函数,求差得之),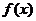 在
在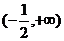 上递增
上递增

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
令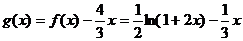
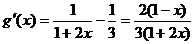 在
在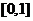 上总有
上总有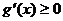 ,即
,即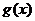 在
在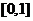 上递增
上递增
当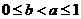 时,
时,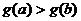
即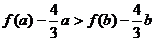
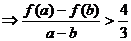
令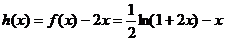 ,由(Ⅱ)知它在
,由(Ⅱ)知它在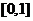 上递减 ∴
上递减 ∴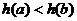 即
即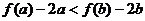
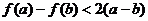 ∵
∵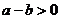
∴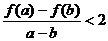 ,综上
,综上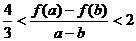 成立,其中
成立,其中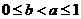 .
.
21. 解:(Ⅰ)在 中,令n=1,可得
中,令n=1,可得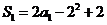 ,即
,即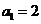
当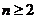 时,
时,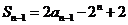 ,则
,则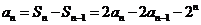
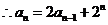 ,即
,即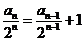
∵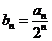 ∴
∴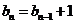 ,即当
,即当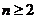 时,
时,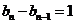
又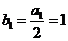 ∴数列
∴数列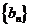 是首项和公差均为1的等差数列
是首项和公差均为1的等差数列
于是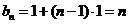
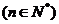 ,
,

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
从而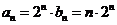
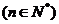
(Ⅱ)由(Ⅰ)得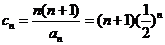 ,
,
所以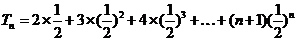
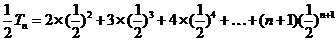
两式相减得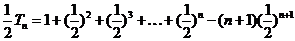
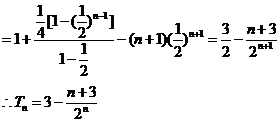
证法1:∵
∴数列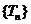 是增数列 故
是增数列 故 ,命题得证.
,命题得证.
证法2:要证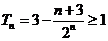 ,即证
,即证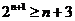
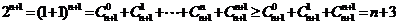 ,命题得证.
,命题得证.
证法3:数学归纳法证明(略).

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
20.解:(Ⅰ)由题意有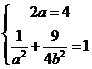 ,解得
,解得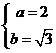
∴椭圆的方程为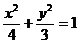
(Ⅱ)设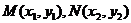 ,由
,由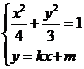
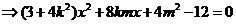
∵直线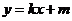 与椭圆有两个交点
与椭圆有两个交点

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
∴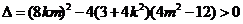 ,即
,即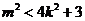
又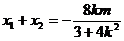
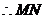 中点
中点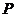 的坐标为
的坐标为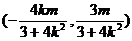
设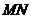 的垂直平分线
的垂直平分线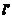 方程:
方程: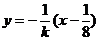
 在
在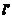 上
上 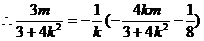 即
即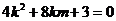
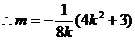
将上式代入得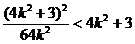
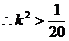
即 或
或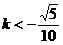
 的取值范围为
的取值范围为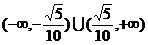 .
.
19.解法1:(Ⅰ)设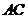 与
与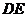 交点为
交点为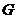 ,延长
,延长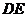 交
交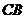 的延长线于点
的延长线于点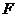 ,
,
则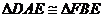 ,∴
,∴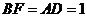 ,∴
,∴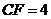 ,∴
,∴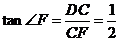 ,
,
又∵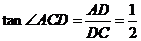 ,∴
,∴ ,
,
 又∵
又∵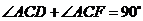 ,∴
,∴ ,
,
∴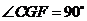 ,∴
,∴


 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
又∵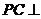 底面
底面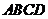 ,∴
,∴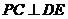 ,∴
,∴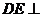 平面
平面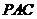 ,
,
∵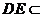 平面
平面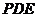 ,∴平面
,∴平面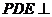 平面
平面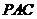
(Ⅱ)连结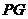 ,过点
,过点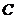 作
作 于
于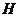 点,取
点,取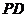 中点
中点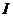 ,连接
,连接 ,易知
,易知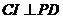
又由(Ⅰ)知平面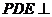 平面
平面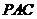 ,且
,且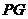 是交线,
是交线,
根据面面垂直的性质,得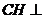 平面
平面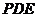 ,
,
由三垂线定理知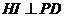
从而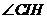 为二面角
为二面角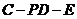 的平面角
的平面角
在等腰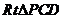 中,
中,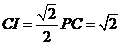 ;
;
在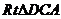 中,
中,
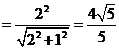 ,
,
在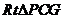 中,
中,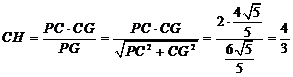
从而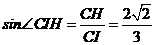 ,则
,则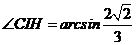
即二面角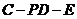 的大小为
的大小为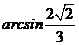
 (Ⅲ)由于
(Ⅲ)由于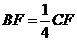 ,所以可知点
,所以可知点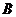 到平面
到平面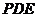 的距离等于点
的距离等于点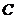 到平面
到平面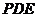 的距离的
的距离的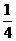 ,即
,即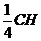 . 在
. 在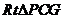 中,
中,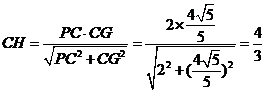 ,
,
从而点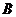 到平面
到平面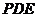 的距离等于
的距离等于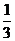
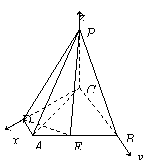
解法2:如图所示,以点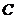 为坐标原点,直线
为坐标原点,直线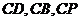 分别为
分别为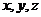 轴,
轴,
建立空间直角坐标系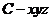 ,则相关点的坐标为
,则相关点的坐标为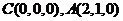
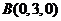 ,
,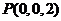 ,
,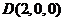 ,
,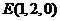 .
.

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
(Ⅰ)由于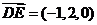 ,
,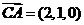 ,
,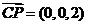 ,
,
所以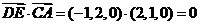 ,
,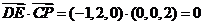 ,
,
所以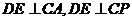 ,
,
而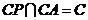 ,所以
,所以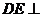 平面
平面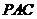 ,∵
,∵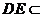 平面
平面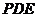 ,
,
∴平面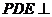 平面
平面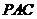
(Ⅱ)设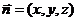 是平面
是平面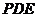 的一个法向量,则
的一个法向量,则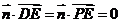 , 由于
, 由于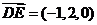 ,
,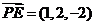 ,所以有
,所以有
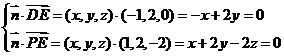 ,令
,令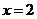 ,则
,则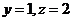 ,即
,即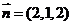 ,易知平面
,易知平面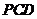 的一个法向量
的一个法向量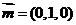
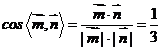 ∴二面角
∴二面角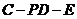 的大小为
的大小为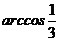
(Ⅲ)由(Ⅱ)知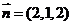 是平面
是平面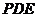 的一个法向量,而
的一个法向量,而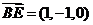 ,
,
所以点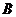 到平面
到平面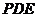 的距离为
的距离为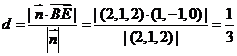
18.解:(Ⅰ)记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件
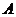 、
、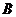 、
、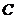 ,则
,则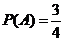 ,且有
,且有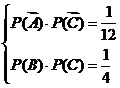 即
即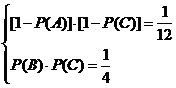

(Ⅱ)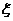 的可能取值:0,1,2,3
的可能取值:0,1,2,3
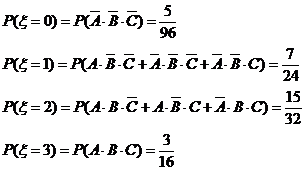
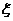 |
0 |
1 |
2 |
3 |
 |
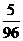 |
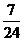 |
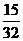 |
 |
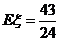 .
.
17.解:(Ⅰ)由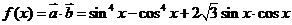
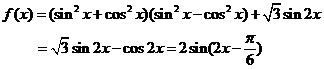
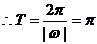
由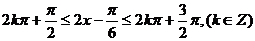


 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
则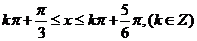
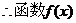 的单调减区间为
的单调减区间为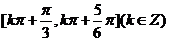
(Ⅱ)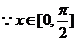 ∴
∴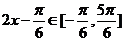
从而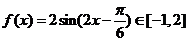
∴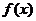 在
在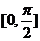 上的最小值为
上的最小值为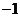 ,此时
,此时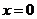 .
.
13、 1 14、
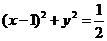 15、
15、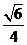 16、①②④
16、①②④
(1~5)CCDCB (6~10)AAABD (11~12)BB
22、(本小题满分14分)已知函数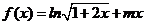 .
.
(Ⅰ)若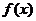 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数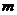 的取值范围;
的取值范围;
(Ⅱ)当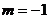 时,求函数
时,求函数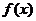 的最大值;
的最大值;
(Ⅲ)当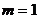 时,且
时,且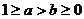 ,证明:
,证明: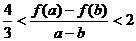 .
.
攀枝花市2010级高三第三次统考数学试题(理科)
21、(本小题满分12分)已知数列 的前n项和
的前n项和
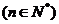 .
.
(Ⅰ)设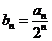 ,求证数列
,求证数列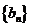 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)令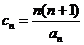 ,
,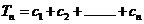 ,求证:
,求证: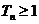
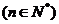 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com