
21.(本小题满分14分) 已知函数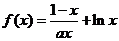
(1)若函数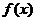 在
在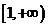 上为增函数,求正实数
上为增函数,求正实数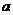 的取值范围;
的取值范围;
(2)当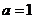 时,求
时,求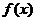 在
在 上的最大值和最小值;
上的最大值和最小值;
(3)当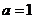 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数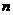 ,都有
,都有
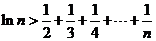
惠州市2010届高三第三次调研考试
20.(本小题满分14分) 已知数列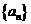 中,
中,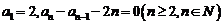 .
.
(1)写出 的值(只写结果)并求出数列
的值(只写结果)并求出数列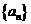 的通项公式;
的通项公式;
(2)设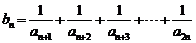 ,若对任意的正整数
,若对任意的正整数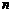 ,当
,当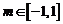 时,不等式
时,不等式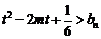 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
19.(本小题满分14分)
已知点 是⊙
是⊙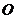 :
: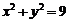 上的任意一点,过
上的任意一点,过 作
作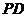 垂直
垂直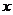 轴于
轴于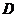 ,动点
,动点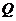 满足
满足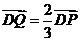 。
。
(1)求动点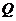 的轨迹方程;
的轨迹方程;
(2)已知点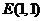 ,在动点
,在动点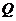 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点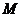 、
、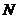 ,使
,使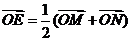 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线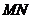 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
18.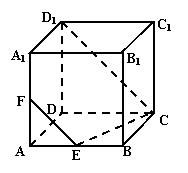 (本小题满分14分) 如图所示,在正方体
(本小题满分14分) 如图所示,在正方体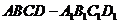 中,E为AB的中点
中,E为AB的中点
(1)若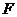 为
为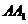 的中点,求证:
的中点,求证:  ∥面
∥面 ;
;
(2) 若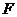 为
为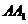 的中点,求二面角
的中点,求二面角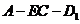 的余弦值;
的余弦值;
(3)若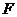 在
在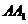 上运动时(
上运动时(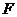 与
与 、
、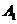 不重合),
不重合),
求当半平面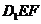 与半平面
与半平面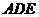 成
成 的角时,线段
的角时,线段 的比.
的比.
17.(本小题满分12分)
在一个圆锥体的培养房内培养了40只蜜蜂,准备进行某种实验,过圆锥高的中点有一个不计厚度且平行于圆锥底面的平面把培养房分成两个实验区,其中小锥体叫第一实验区,圆台体叫第二实验区,且两个实验区是互通的。假设蜜蜂落入培养房内任何位置是等可能的,且蜜蜂落入哪个位置相互之间是不受影响的。
(1)求蜜蜂落入第二实验区的概率;
(2)若其中有10只蜜蜂被染上了红色,求恰有一只红色蜜蜂落入第二实验区的概率;
(3)记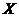 为落入第一实验区的蜜蜂数,求随机变量
为落入第一实验区的蜜蜂数,求随机变量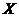 的数学期望
的数学期望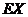 。
。
16.(本小题满分12分)
已知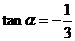 ,
,

(1)求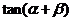 的值;
的值;
(2)求函数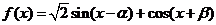 的最大值.
的最大值.
(二)选做题(14 -15题,考生只能从中选做一题;两道题都做的,只记第一题的分)
14. (坐标系与参数方程选做题)若P是极坐标方程为
(坐标系与参数方程选做题)若P是极坐标方程为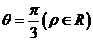 的直线与参数方程为
的直线与参数方程为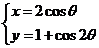 (
( 为参数,且
为参数,且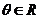 )的曲线的交点,则P点的直角坐标为
.
)的曲线的交点,则P点的直角坐标为
.
15.(几何证明选讲选做题)如图,平行四边形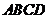 中,
中,
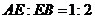 ,
, 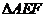 的面积为6,
的面积为6,
则 的面积为
.
的面积为
.
(一)必做题(9-13题)
9. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如,明文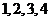 对应密文
对应密文 . 当接收方收到密文
. 当接收方收到密文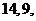
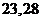 时,则解密得到的明文为
.
时,则解密得到的明文为
.
10. 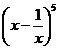 的展开式中含
的展开式中含 项的二项式系数为
.
项的二项式系数为
.
11. 若抛物线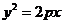 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则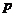 的 值为
.
的 值为
.
12. 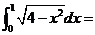 .
.
13. 已知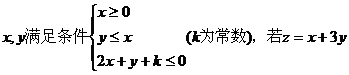 的最大值为8,则
的最大值为8,则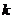 = .
= .
8.给出定义:若函数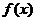 在
在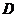 上可导,即
上可导,即 存在,且导函数
存在,且导函数 在
在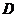 上也可导,则称
上也可导,则称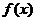 在
在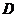 上存在二阶导函数,记
上存在二阶导函数,记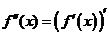 ,若
,若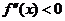 在
在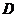 上恒成立,则称
上恒成立,则称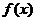 在
在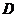 上为凸函数。以下四个函数在
上为凸函数。以下四个函数在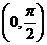 上不是凸函数的是( )
上不是凸函数的是( )
A.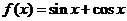 B.
B.
C.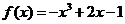 D.
D.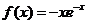
7. 用若干个体积为1的正方体搭成一个几何体,其正视图、侧视图都是如图所示 的图形,则这个几何体的最大体积与最小体积的差是( ).
A.6 B.7 C.8 D.9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com