
12.一元二次方程根的分布理论。
(1)实系数方程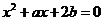 的一根大于0且小于1,另一根大于1且小于2,则
的一根大于0且小于1,另一根大于1且小于2,则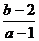 的取值范围是_________(答:(
的取值范围是_________(答:(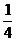 ,1))
,1))
(2)不等式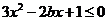 对
对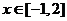 恒成立,则实数
恒成立,则实数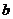 的取值范围是____(答:
的取值范围是____(答: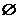 )。
)。
11. 对于方程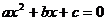 有实数解的问题。
有实数解的问题。
(1)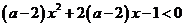 对一切
对一切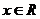 恒成立,则
恒成立,则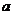 的取值范围是_______(答:
的取值范围是_______(答: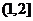 );
);
(2)若在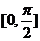 内有两个不等的实根满足等式
内有两个不等的实根满足等式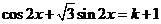 ,则实数
,则实数 的范围是_______.(答:
的范围是_______.(答: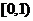 )
)
10. 一元二次不等式的解集:
(2009福建卷理)已知全集U=R,集合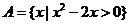 ,则
,则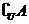 等于
等于
A. { x ∣0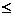 x
x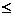 2}
B { x ∣0<x<2}
2}
B { x ∣0<x<2}
C. { x ∣x<0或x>2}
D { x ∣x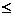 0或x
0或x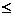 2}
2}
[答案]:A
[解析]∵计算可得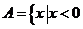 或
或 ∴
∴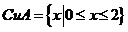 .故选A
.故选A
(2009安徽卷理)若集合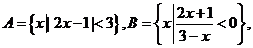 则A∩B是
则A∩B是
(A) 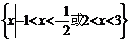 (B)
(B) 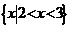 (C)
(C)
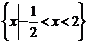 (D)
(D) 
[解析]集合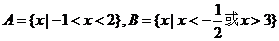 ,∴
,∴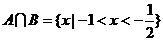 选D
选D
9. 一元一次不等式的解法:
已知关于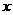 的不等式
的不等式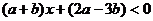 的解集为
的解集为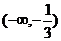 ,则关于
,则关于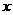 的不等式
的不等式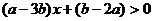 的解集为_______(答:
的解集为_______(答: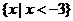 )
)
8.充要条件:
(1)(2009四川卷文)已知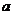 ,
,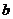 ,
,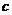 ,
,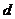 为实数,且
为实数,且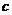 >
>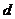 .则“
.则“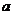 >
>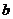 ”是“
”是“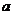 -
-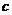 >
>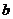 -
-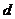 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
[答案]B
[解析]显然,充分性不成立.又,若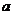 -
-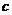 >
>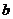 -
-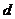 和
和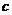 >
>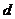 都成立,则同向不等式相加得
都成立,则同向不等式相加得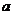 >
>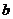
即由“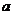 -
-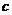 >
>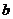 -
-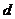 ”
”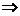 “
“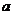 >
>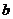 ”
”
(2)设命题p: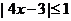 ;命题q:
;命题q: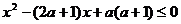 。若┐p是┐q的必要而不充分的条件,则实数a的取值范围是
(答:
。若┐p是┐q的必要而不充分的条件,则实数a的取值范围是
(答: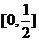 )
)
7.复合命题真假的判断:
(2009重庆卷文)命题“若一个数是负数,则它的平方是正数”的逆命题是( )
A.“若一个数是负数,则它的平方不是正数” B.“若一个数的平方是正数,则它是负数”
C.“若一个数不是负数,则它的平方不是正数” D.“若一个数的平方不是正数,则它不是负数”
[答案]B
解析 因为一个命题的逆命题是将原命题的条件与结论进行交换,因此逆命题为“若一个数的平方是正数,则它是负数”。
6.补集思想:
已知函数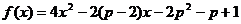 在区间
在区间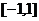 上至少存在一个实数
上至少存在一个实数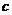 ,使
,使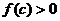 ,求实数
,求实数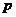 的取值范围。 (答:
的取值范围。 (答: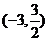 )
)
5.集合的代表元素:
(1)设集合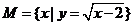 ,集合N=
,集合N=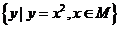 ,则
,则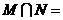 ___(答:
___(答: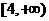 );
);
(2)(2009湖北卷理)已知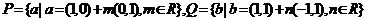 是两个向量集合,则
是两个向量集合,则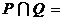
A.{(1,1)} B. {(-1,1)} C. {(1,0)} D. {(0,1)}
[答案]A
[解析]因为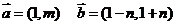 代入选项可得
代入选项可得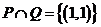 故选A.
故选A.
4.运算性质:设全集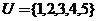 ,若
,若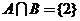 ,
,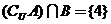 ,
,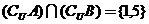 ,则A=_____,B=___.(答:
,则A=_____,B=___.(答: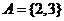 ,
,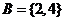 )
)
3. 韦恩图:(2009年广东卷文)已知全集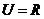 ,则正确表示集合
,则正确表示集合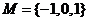 和
和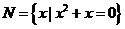 关系的韦恩(Venn)图是
关系的韦恩(Venn)图是
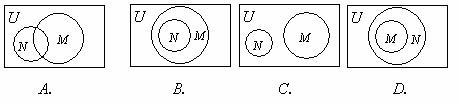
[答案]B
[解析]由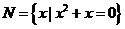 ,得
,得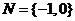 ,则
,则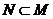 ,选B.
,选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com