
1.某学校生物兴趣小组开展了“调查人群中的遗传病”的实践活动,以下调查方法或结论不太合理的是
A.调查时,最好选取群体中发病率相对较高的多基因遗传病,如原发性高血压、冠心病等
B.调查时应分多个小组、对多个家庭进行调查,以获得足够大的群体调查数据
C.为了更加科学、准确调查该遗传病在人群中的发病率,应特别注意随机取样
D.若调查结果是男女患病比例相近,且发病率较高,则可能是常染色体显性遗传病
17. 本题主要考查概率、统计等基础知识,考查数据处理能力、运算求解能力,考查分类与整
合思想、化归与转化思想.
解:(Ⅰ)∵3名工人选择的项目均为A类工程的概率 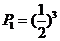 ,……………………(1分)
,……………………(1分)
均为B类工程的概率  ,
………………………(2分)
,
………………………(2分)
均为C类工程的概率 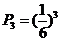 , ………………………(3分)
, ………………………(3分)
∴他们选择的项目所属工程类别相同的概率 . …………(5分)
. …………(5分)
(Ⅱ)设三名工人中选择项目属于A类工程的人数为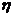 ,则
,则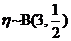 ,
,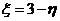 .
.
………………………(7分)
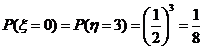 , ………………………(8分)
, ………………………(8分)
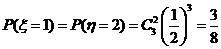 , ………………………(9分)
, ………………………(9分)
 , ………………………(10分)
, ………………………(10分)
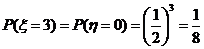 . ………………………(11分)
. ………………………(11分)

 (Ⅱ)过O作AD的平行线为x轴,OB、OP分别为y、z轴,建立空间直角坐标系,则
(Ⅱ)过O作AD的平行线为x轴,OB、OP分别为y、z轴,建立空间直角坐标系,则


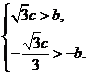 ………………………(6分)
………………………(6分)
即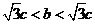 ,∴
,∴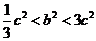 ,∴
,∴ .
.
故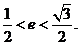 ………………………(8分)
………………………(8分)
(3)直线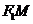 与直线
与直线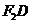 的交点在定直线
的交点在定直线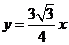 上, ………………………(9分)
上, ………………………(9分)
证明如下:由(1)有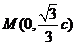 ,因为A、B、M、O、C六点均匀分布,则必有
,因为A、B、M、O、C六点均匀分布,则必有


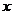 |
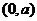 |
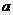 |
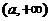 |
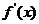 |
+ |
0 |
- |
 |
↗ |
|
↘ |
故 在
在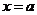 处取得极大值.
处取得极大值.
要使 在区间
在区间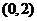 上无极值,则
上无极值,则 .
.
综上所述,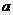 的取值范围是
的取值范围是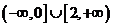 .
………………………(9分)
.
………………………(9分)
(Ⅲ)由(Ⅱ)知,当 时,
时,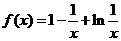 在
在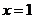 处取得最大值
处取得最大值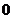 .
.
即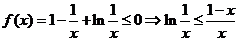 .
.
令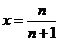 ,则
,则 ,即
,即 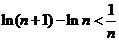 ,
,
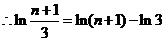


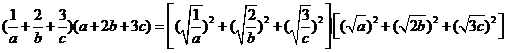
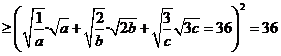 . ………………………(5分)
. ………………………(5分)
又 ,
, 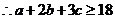 . 当且仅当
. 当且仅当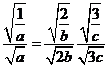 ,
,
即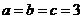 时等式成立.
时等式成立.
∴当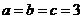 时,
时,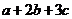 取得最小值18. ………………………(7分)
取得最小值18. ………………………(7分)
21. 本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题做答,满分14分,如果多做,则按所做的前两题计分. 作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中
(Ⅰ)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵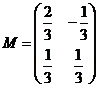 ,
,
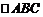 的顶点为A(0,0),B(2,0),C(1,2),求
的顶点为A(0,0),B(2,0),C(1,2),求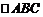
在矩阵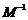 的变换作用下所得
的变换作用下所得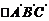 的面积.
的面积.
(Ⅱ)(本小题满分7分)选修4-4:坐标系与参数方程
极坐标的极点是直角坐标系原点,极轴为X轴正半轴,直线l的参数方程为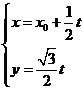
(t为参数)。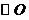 的极坐标方程为
的极坐标方程为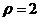 ,若直线l与
,若直线l与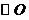 相切,求实数
相切,求实数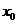 的值。
的值。
(Ⅲ)(本小题满分7分)选修4-5:不等式选讲
已知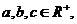 且
且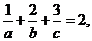 求
求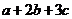 的最小值及取得最小值时
的最小值及取得最小值时 的值。
的值。

 ∴
∴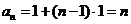 .
………………………(5分)
.
………………………(5分)
(2)由(1)得
若 ,则
,则
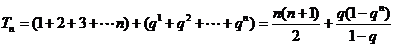
………………………(9分)
若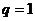 则
则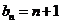 ,
,
 ………………………(13分)
………………………(13分)
20. (本题满分14分)
已知函数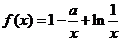 (
(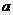 为实常数)。
为实常数)。
(Ⅰ)当 时,求函数
时,求函数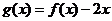 的单调区间;
的单调区间;
(Ⅱ)若函数 在区间
在区间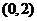 上无极值,求
上无极值,求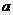 的取值范围;
的取值范围;
(Ⅲ)已知 且
且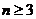 ,求证:
,求证: 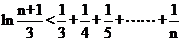 .
.
19. (本题满分13分)
平面直角坐标系xOy中,已知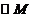 经过点
经过点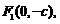
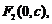
 三点,其中
三点,其中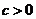 .
.
(Ⅰ)求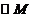 的标准方程(用含
的标准方程(用含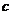 的式子表示);
的式子表示);
(Ⅱ)已知椭圆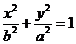 (其中
(其中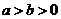 ,
,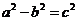 )的左、右顶点分别为D、
)的左、右顶点分别为D、
B, 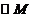 与X轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧,
与X轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧,
求椭圆离心率的取值范围;
(Ⅲ)若A、B、M、O、C、D(O为坐标原点)依次均匀分布在X轴上,问直线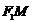 与直线
与直线 的交点是否在一条定直线上?如果是,请求出这条定直线的方程,如果不是,请说明理由
的交点是否在一条定直线上?如果是,请求出这条定直线的方程,如果不是,请说明理由
18. (本题满分13分)
(本题满分13分)
已知四棱锥P-ABCD的直观图(如图1)
及左视图(如图2),底面ABCD是边长
为2的正方形,平面PAB⊥平面ABCD,
PA=PB。
(Ⅰ)求证:AD⊥PB;
(Ⅱ)求异面直线PD与AB所成角的余弦值;
(Ⅲ)求平面PAB与平面PCD所成锐二面角
|
17. (本小题满分13分)
某地决定新建A,B,C三类工程,A,B,C三类工程所含项目的个数分别占总项目数的
 (总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(Ⅰ)求他们选择的项目所属工程类别相同的概率;
(Ⅱ)记 为3人中选择的项目属于B类工程或C类工程的人数,求
为3人中选择的项目属于B类工程或C类工程的人数,求 的分布列及数学期望.
的分布列及数学期望.
16. (本小题满分13分)
在等差数列 中,
中,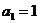 ,
,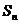 为前n项和,且满足
为前n项和,且满足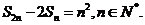
(Ⅰ)求 及
及 的通项公式;
的通项公式;
(Ⅱ)记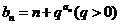 ,求
,求 的前n项和
的前n项和
15. 现有5男5女共10个小孩设想做如下游戏:先让4个小孩(不全为男孩)等距离站在一个圆周的4个位置上,如果相邻两个小孩同为男孩或同为女孩,则在他(她)们中间站进一个男孩,否则站进一个女孩,然后让原来的4个小孩暂时退出,即算一次活动.这种活动按上述规则继续进行,直至圆周上所站的4个小孩都为男孩为止,则这样的活动最多可以进行 次。
14. 已知曲线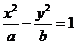 与直线
与直线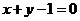 相交于
相交于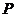 、
、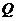
两点,且 (
(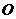 为原点),则
为原点),则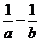 的值为
。
的值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com