
3.在漂流探险中,探险者驾驶摩托艇想上岸休息,假设江岸是平直的,江水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,原来地点A离岸边最近处0的距离为d。如果探险者想在最短时间内靠岸,则摩托艇登陆的地点离0点的距离为( )
A. B.0 C.
B.0 C.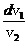 D.
D. 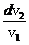
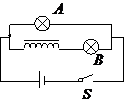 4.如图所示,电源的电动势为E,内阻r不能忽略。A、B是两个相同的小灯泡,线圈的自感系数相当大,直流电阻不可忽略。关于这个电路以下说法正确的是(
)
4.如图所示,电源的电动势为E,内阻r不能忽略。A、B是两个相同的小灯泡,线圈的自感系数相当大,直流电阻不可忽略。关于这个电路以下说法正确的是(
)
A.开关闭合到电路中电流稳定的时间内,A灯立刻亮,而后逐渐变暗,最后亮度稳定
B.开关闭合到电路中电流稳定的时间内,B灯立刻亮,而后逐渐变暗,最后亮度稳定
C.电路稳定后,突然断开开关,A灯会闪亮一下再熄灭
D.电路稳定后,突然断开开关,电流会自左向右通过A灯
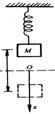
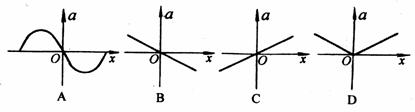
2.如图所示,轻弹簧下端挂一个质量为M的重物,平衡后静止在原点O。现令其在O点上下做简谐运动,下列四幅图像能正确反映重物的加速度a随位移x变化关系的是( )(沿x轴正方向的加速度为正)。
1. 如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔。质量为m的小球套在圆环上。一根细线的下端系着小球,上端穿过小孔用手拉住。现拉动细线,使小球沿圆环缓慢上移。在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是(
)
如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔。质量为m的小球套在圆环上。一根细线的下端系着小球,上端穿过小孔用手拉住。现拉动细线,使小球沿圆环缓慢上移。在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是(
)
A.F不变,N增大 B.F不变,N 减小
C.F减小,N不变 D.F增大,N减小
70、如图所示,某要乘雪橇从雪坡经A点滑到B点,接着沿水平路面滑至C点停止。人与雪橇的总质量为70kg。右表中记录了沿坡滑下过程中的有关数据,开始时人与雪橇距水平路面的高度h=20m,请根据右表中的数据解决下列问题:
(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力的大小。
(3)人与雪橇从B运动到C的过程中所对应的距离。(取g=10m/s2)
|
位置 |
A |
B |
|
||
|
速度(m/s) |
2.0 |
12.0 |
0 |
||
|
时刻(s) |
0 |
4.0 |
10.0 |
解:(1)从A到B的过程中,人与雪橇损失的机械能为
 (2分)
(2分)
代入数据解得△E=9.1×103J (1分)
(2)人与雪橇在BC段做减速运动的加速度大小 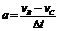 (1分)
(1分)
根据牛顿第二定律有 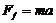 (1分)
(1分)
解得  N (2分)
N (2分)
(3)由动能定得得 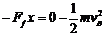 (2分)
(2分)
代入数据解得 x=36m (1分)
69、如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑雪道滑下,从B点水平飞出后又落在与水平面成倾角 =
= 的斜坡上C点.已知AB两点间的高度差为h=25m,B、C两点间的距离为s=75m,已知sin370=0.6,取g=10m/s2,求:
的斜坡上C点.已知AB两点间的高度差为h=25m,B、C两点间的距离为s=75m,已知sin370=0.6,取g=10m/s2,求:
 (1)运动员从B点水平飞出时的速度大小;
(1)运动员从B点水平飞出时的速度大小;
(2)运动员从A点到B点的过程中克服摩擦力做的功.
解:(1)由B到C平抛运动的时间为t
竖直方向:hBc=ssin37o=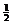 gt2 (1)
(3分)
gt2 (1)
(3分)
水平方向:scos370=vBt (2) (3分)
代得数据,解(1)(2)得vB=20m/s (3)(2分)
(2)A到B过程,由动能定理有
mghAB+wf=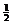 mvB2 (4)
(3分)
mvB2 (4)
(3分)
代人数据,解(3)(4)得 wf =-3000J (2分)
所以运动员克服摩擦力所做的功为3000J
68、如图所示,光滑坡道顶端距水平面高度为h,质量为m的小物块A 从坡道顶端由静止滑下,进入水平面上的滑道,经过O点时无机械能损失,为使A制动,将轻弹簧的一端固定在竖直墙上的M点,另一端恰位于滑道的末端O点。已知在OM段,物块A与水平面间的动摩擦因数均为μ,其余各处的摩擦不计,重力加速度为g,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量d时的弹性势能 (设弹簧处于原长时弹性势能为零)
(3)若物块A能够被弹回到坡道上,则它能够上升的最大高度是多少?

(1)由机械能守恒定律得  (2分)
(2分)
解得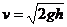 (1分)
(1分)
(2)在水平滑道上物块A克服摩擦力所做的功为
 (1分)
(1分)
由能量守恒定律得 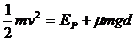 (2分)
(2分)
以上各式联立求解得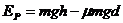 (1分)
(1分)
(3)物块A被弹回的过程中,克服摩擦力所做的功仍为
 (1分)
(1分)
由能量守恒定律得 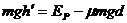 (1分)
(1分)
解得物块A能够上升的最大高度为: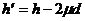 (1分)
(1分)
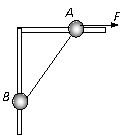
67、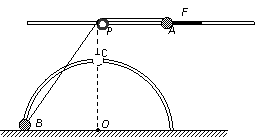 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A。半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2。现给小球A一个水平向右的恒力F=55N。求:
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A。半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2。现给小球A一个水平向右的恒力F=55N。求:
(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;
(2)小球B运动到C处时的速度大小;
(3)小球B被拉到离地多高时与小球A速度大小相等。
(1)小球B运动到P点正下方过程中的位移为
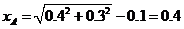 (m)(2分)
(m)(2分)
得:WF=FxA=22J(2分)
(2)由动能定理得
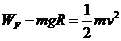
代入数据得:v=4m/s(4分)
⑶当绳与圆环相切时两球的速度相等。
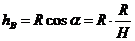 =0.225m(4分)
=0.225m(4分)
66、如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数=0.20,杆的竖直部分光滑,两部分各套有质量分别为2.0kg和1.0kg的小球A和B,A、B间用细绳相连,初始位置OA=1.5m,OB=2.0m,g取10 m/s2,则
(1)若用水平拉力F1沿杆向右缓慢拉A,使之移动0.5m,该过程中A受到的摩擦力多大?拉力F1做功多少?
(2)若小球A、B都有一定的初速度,A在水平拉力F2的作用下,使B由初始位置以1.0m/s的速度匀速上升0.5m,此过程中拉力F2做功多少?

(1)A、B小球和细绳整体竖直方向处于平衡,A受到水平的弹力为:
N=(mA+mB)g (2分)
则A受到的摩擦力为Ff=(mA+mB)g
代入数字得:Ff=6N (2分)
由几何关系,sB=0.5m (2分)
由能量关系,拉力F1做功为:
W1=Ffs+mBgsB;
代入数字得:W1=20 J (2分)
(2)设细绳与竖直方向的夹角为,因细绳不可伸长,所以有
vBcos=vAsin (2分)
则: m/s
m/s
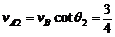 m/s (2分)
m/s (2分)
设拉力F2做功为W2,对系统由能量关系得:
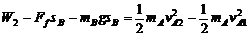 (2分)
(2分)
代入数字得W2=6.8 J (2分)
65、如图所示,电场极板AB间有电场强度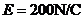 的匀强电场,一带电量
的匀强电场,一带电量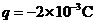 的小球开始时静止在电场中的
的小球开始时静止在电场中的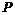 点,靠近电场极板B处有一挡板S,小球与挡板S的距离
点,靠近电场极板B处有一挡板S,小球与挡板S的距离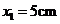 ,与
,与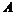 板距离
板距离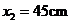 ,小球的重力不计.在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的K倍,已知
,小球的重力不计.在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的K倍,已知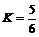 ,碰撞过程中小球的机械能没有损失.
,碰撞过程中小球的机械能没有损失.
(1)求小球第一次到达挡板S时的动能;
(2)求小球第一次与挡板S相碰后向右运动的距离;
(2)小球与挡板S经过多少次碰撞后,才能运动到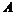 板?
板?
解:(1)小球第一次到达挡板时,由动能定理得
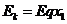 =0.02J
(3分)
=0.02J
(3分)
(2)设小球与挡板相碰后向右运动s,则
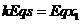 (2分)
(2分)
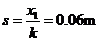 (1分)
(1分)
(3)分析题意可知,每次碰后向右 运动的距离是前一次的1/k,
运动的距离是前一次的1/k,
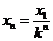
 (4分)
(4分)
n=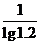 =13
(2分)
=13
(2分)
64、如图所示,一倾角为30°的光滑斜面底端有一与斜面垂直的固定挡板M,物块A、B之间用一与斜面平行轻质弹簧连结,现用力缓慢沿斜面向下推动物块B,当弹簧具有5J弹性势能时撤去推力释放物块B;已知A、B质量分别为mA=5kg、mB=2kg,弹簧的弹性势能表达式为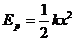 ,其中弹簧的劲度系数k=
,其中弹簧的劲度系数k=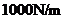 ,x为弹簧形变量,
,x为弹簧形变量, ,求:
,求:
(1)当弹簧恢复原长时,物块B的速度大小;
(2)物块A刚离开挡板时,物块B的动能.
解:(1)当Ep =5J时,弹簧压缩x1,由 得x1=0.1m (2分)
得x1=0.1m (2分)
当弹簧恢复原长时,由机械能守恒可得
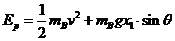 (2分)
(2分)
v=2m/s (1分)
(2)当物块A刚离开挡板时,弹簧伸长x2,
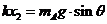 (1分)
(1分)
x2=0.025m (1分)
由系统机械能守恒得
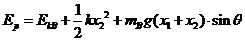 (2分)
(2分)
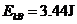 (1分)
(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com