
20.(本小题满分12分)
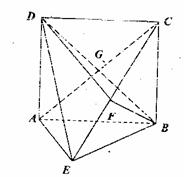 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE。
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE。
(1)求证:AE⊥平面BCE;
(2)求证:AE//平面BFD;
(3)求三棱锥C-BGF的体积。
19.(本小题满分12分)
已知向量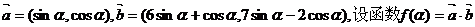
(1)求函数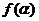 的值;
的值;
(2)在锐角三角形ABC中,角A、B、C的对边分别为a、b、c,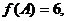 且
且 的面积为3,
的面积为3,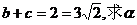 的值。
的值。
18.(本小题满分12分)
高考数学考试中共有12道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的。评分标准规定:“在每小题给出的上个选项中,只有一项是符合题目要求的,答对得5分,不答或答错得0分”。某考生每道选择都选出一个答案,能确定其中有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项错误的,有一道题可能判断一个选项是错误的,还有一道题因不理解题意只能乱猜。试求出该考生的选择题:
(1)得40分的概率;
(2)得多少分的概率最大?
(3)所得分数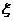 的数学期望。
的数学期望。
17.(本小题满分12分)
已知函数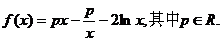
(1)若函数 在其定义域内为单调递增函数,求实数p的取值范围。
在其定义域内为单调递增函数,求实数p的取值范围。
(2)若函数 ,若在[1,e]上至少存在一个x的值使
,若在[1,e]上至少存在一个x的值使 成立,求实数p的取值范围。
成立,求实数p的取值范围。
16.若AB是过二次曲线中心的任一条弦,M是二次曲线上异于A,B的任一点,且AM,BM均与坐标轴不平行,则对于椭圆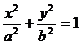 有
有 类似地,对于双曲线
类似地,对于双曲线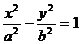 有
有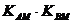 =
。
=
。
15.若关于x,y方程组 有两个不同的解,则实数m的取值范围是
有两个不同的解,则实数m的取值范围是
。
14.对于集合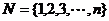 及其它的每一个排空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1,2,4,6,9}的交替和是9-6+4-2+1=6,集合{5}的交替和为5,等等。当集合N中的n=2时,集合
及其它的每一个排空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1,2,4,6,9}的交替和是9-6+4-2+1=6,集合{5}的交替和为5,等等。当集合N中的n=2时,集合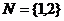 的所有非空子集为{1},{2},{1,2},则它的“交替和”的总和
的所有非空子集为{1},{2},{1,2},则它的“交替和”的总和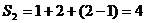 ,请你尝试对n=3,n=4的情况,计算它的“交替和”的总和
,请你尝试对n=3,n=4的情况,计算它的“交替和”的总和 ,并根据其结果猜测集合
,并根据其结果猜测集合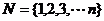 的每一个非空子集的“交替和”的总和
的每一个非空子集的“交替和”的总和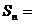
。
13.若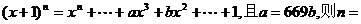 。
。
12.已知平面内一点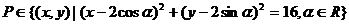 ,则满足条件的点P在平面内所组成的图形的面积是 ( )
,则满足条件的点P在平面内所组成的图形的面积是 ( )
A.36π B.32π C.16π D.4π
第Ⅱ卷(非选择题,共90分)
11.若关于x的方程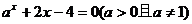 的所有根记作
的所有根记作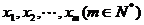 ,关于x的方程
,关于x的方程 的所有根记作
的所有根记作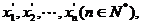 则
则
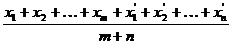 的值为 ( )
的值为 ( )
A.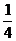 B.
B.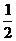 C.1 D.2
C.1 D.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com