
2、以第1,2,3周期的元素为例,了解原子核外电子排布规律。
19.(本小题满分13分)
已知椭圆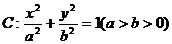 的离心率为
的离心率为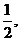 以原点O为圆心,椭圆的短半轴长为半径的圆与直线
以原点O为圆心,椭圆的短半轴长为半径的圆与直线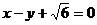 相切。
相切。
(I)求椭圆C的方程;
(II)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E,证明直线AE与x轴交于定点Q;
(III)在(II)条件下,过点Q的直线与椭圆C交于M,N两点,求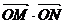 的取值范围。
的取值范围。
17.(本小题满分14分)
如图1所示,在边长为12的正方形ADD1A1中,点B、C在线段AD上,且AB=3,BC=4,作BB1//AA1,分别交A1D1,AD1于点B1,P,作CC1//AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1。
(I)求证:AB⊥平面BCC1B1;
(II)求四棱锥A-BCQP的体积;
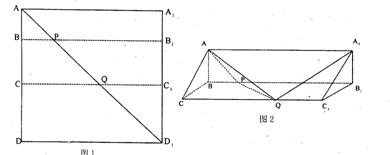 (III)求平面PQA与平面BCA所成锐二面角的余弦值。
(III)求平面PQA与平面BCA所成锐二面角的余弦值。
16.(本小题满分13分)
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下:
(I)计算样本的平均成绩及方差;
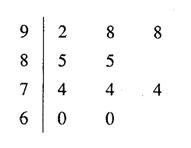 (II)现从这10个样本中随机抽出2名学生的成绩,设选出学生的分数为90分以上的人数为X,求随机变量X的分布列和均值。
(II)现从这10个样本中随机抽出2名学生的成绩,设选出学生的分数为90分以上的人数为X,求随机变量X的分布列和均值。
15.(本小题满分13分)
设函数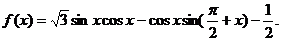
(I)求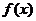 的最小正周期;
的最小正周期;
(II)当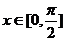 时,求函数
时,求函数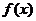 的最大值和最小值。
的最大值和最小值。
14.如果对任意一个三角形,只要它的三边长a、b、c都在函数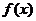 的定义域内,就有
的定义域内,就有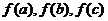 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称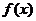 为“JI型函数”,那么下列函数:
为“JI型函数”,那么下列函数:
①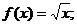 ②
②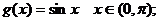 ③
③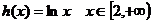 ,
,
是“JI型函数”的序号为 .
13.直线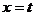 过双曲线
过双曲线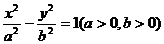 的右焦点且与双曲线的两条渐近线分别交于A、B两点,若原点在以AB为直径的圆外,则双曲线离心率的取值范围是 。
的右焦点且与双曲线的两条渐近线分别交于A、B两点,若原点在以AB为直径的圆外,则双曲线离心率的取值范围是 。
12.圆的极坐标方程为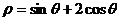 ,将其化成直角坐标方程为
,圆心的直角坐标为
。
,将其化成直角坐标方程为
,圆心的直角坐标为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com