
6.解依题: ,
, …2分
…2分

做差得

得
 …4分
…4分
又因为
解得 …6分
…6分
故 …9分
…9分
故 …12分
…12分
5.(1)由8x f(x)
f(x) 4(x2+1),∴f(1)=8,f(-1)=0,∴b=4
4(x2+1),∴f(1)=8,f(-1)=0,∴b=4
又8x f(x)
f(x) 4(x2+1) 对
4(x2+1) 对 恒成立,∴a=c=2 f(x)=2(x+1)2
恒成立,∴a=c=2 f(x)=2(x+1)2
(2)∵g(x)= =
= ,D={x︱x
,D={x︱x -1
}
-1
}
X1= ,x2=
,x2= ,x3=
,x3= -
- ,x4=-1,∴M={
,x4=-1,∴M={ ,
, ,-
,- ,-1}
,-1}

4. (1)当x∈[-1,0)时, f(x)= f(-x)=loga[2-(-x)]=loga(2+x).
当x∈[2k-1,2k),(k∈Z)时,x-2k∈[-1,0], f(x)=f(x-2k)=loga[2+(x-2k)].
当x∈[2k,2k+1](k∈Z)时,x-2k∈[0,1], f(x)=f(x-2k)=loga[2-(x-2k)].
故当x∈[2k-1,2k+1](k∈Z)时 , f(x)的表达式为
, f(x)的表达式为
|
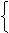 loga[2+(x-2k)],x∈[2k-1,2k),
loga[2+(x-2k)],x∈[2k-1,2k),
loga[2-(x-2k)],x∈[2k,2k+1].
(2)∵f(x)是以2为周期的周期函数,且为偶函数,∴f(x)的最大值就是当x∈[0,1]时f(x)的最大值,∵a>1,∴f(x)=loga(2-x)在[0,1]上是减函数,
∴[f(x)]max= f(0)= =
= ,∴a=4.
,∴a=4.
当x∈[-1,1]时,由f(x)> 得
得
或 得
得
∵f(x)是以2为周期的周期函数,
∴f(x)> 的解集为{x|2k+
的解集为{x|2k+ -2<x<2k+2-
-2<x<2k+2- ,k∈Z
,k∈Z
3.(I) ……1分
……1分
根据题意, …………4分
…………4分
解得 . …………7分
. …………7分
(II)因为 ……7分
……7分
(i) 时,函数
时,函数 无最大值,
无最大值,
不合题意,舍去. …………11分
(ii) 时,根据题意得
时,根据题意得

解之得 …………13分
…………13分
 为正整
为正整 数,
数, =3或4. …………14分
=3或4. …………14分
2.(1)当0<t≤10时,
 是增函数,且f(10)=240
是增函数,且f(10)=240
当20<t≤40时, 是减函数,且f(20)=240 所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。(3)当0<t≤10时,令
是减函数,且f(20)=240 所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。(3)当0<t≤10时,令 ,则t=4 当20<t≤40时,令
,则t=4 当20<t≤40时,令 ,则t≈28.57
,则t≈28.57
则学生注意力在180以上所持续的时间28.57-4=24.57>24
从而教师可以第4分钟至第28.57分钟这个时间段内将题讲完。
1.(1)由题意 ,
, =1又a>0,所以a=1.
=1又a>0,所以a=1.
(2)
 g(x)=
g(x)= ,当
,当 时,
时,

 =
= ,无
,无 递增区间;当x<1时,
递增区间;当x<1时,

 =
= ,它的递增区间是
,它的递增区间是 .
.
综上知:

 的单调递增区间是
的单调递增区间是 .
.
10.(12分)设 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(1)若 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且 ,求点
,求点 的作标;
的作标;
(2)设过定点 的直线
的直线 与椭圆交于同的两点
与椭圆交于同的两点 、
、 ,且
,且 为锐角(其中
为锐角(其中 为作标原点),求直线
为作标原点),求直线 的斜
的斜 率
率 的取值范围.
的取值范围.
9.(12分)已知函数 在
在 处取得极值,
处取得极值,
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围.
的取值范围.
8. (12分)已知以点P为圆心的圆过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C、D,且|CD|= .
.
(1) 求直线CD的方程;
(2)求圆P的方程;
(3)设点Q在圆P上,试探究使△QAB的面积为8的点Q共有几个?证明你的结论.
7. (12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,
(12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中, 是
是
 的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
 (1)求出该几何体的体积;
(1)求出该几何体的体积;
 (2)求证:EM∥平面ABC;
(2)求证:EM∥平面ABC;
 (3)试问在棱DC上是否存在点N,使NM⊥平面
(3)试问在棱DC上是否存在点N,使NM⊥平面 ? 若存在,确定点N的位置;若不存在,请说明理由.
? 若存在,确定点N的位置;若不存在,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com