6．为了除去NaCl溶液中的少量Fe₂(SO₄)₃杂质，最好选用　 (　 )

　　 A、 BaCl₂　　　 B、 NaOH　　　 C、 Ca(OH)₂　　　 D、 Ba(OH)₂

5．能量守恒是自然界的基本规律之一。下列能量转化过程中，化学能转化为电能的是(　 )

　　 A、 用潮汐发电　　　　　　 B、 用电灯照明

　　 C、 用干电池做电源　　　 D、 用电动机带动水泵将水抽到高处

4．下列化学方程式或电离方程式正确的是　　　　 (　 )

　　 A、 Cu+2AgCl＝CuCl₂+2Ag　　　　　

B、 KHSO₄＝K⁺+H⁺+so²⁺₄

　　 C、 C+CuOCO₂+Cu

D、 Mg(OH)₂+CuSO₄＝MgSO₄+Cu(OH)₂¯

3．日常生活中人们常喝纯净水，市场上出售的纯净水有一些是蒸馏水。对于这一类纯净水的下列说法，正确的是　　 (　 )

　　 A、 它能够导电　 B、 它含有人体所需的矿物质和多种微量元素

　　 C、 它的pH＝0　 D、 它清洁、纯净，但长期饮用对健康无益

2．下列变化中，属于化学变化的是　　　　　　 (　 )

　　 A、 用久了的白炽灯灯泡壁上，产生一层黑色物质

　　 B、 工业上用液态空气制取氧气

　　 C、 在云层中撒布干冰进行人工降雨

　　 D、 用石灰浆抹的墙壁，过一段时间后变得很坚固

1．美国和日本的三位科学家以导电有机高分子材料的研究成果荣获2000年诺贝尔化学奖，在其相关技术中用碘来掺杂聚合物，使其导电能力增强10⁷倍，具有金属般的导电能力。碘(I₂)属于　　　　　　　　 　　　　　　(　 )

　　 A、 金属单质　　　 B、 非金属单质　　 C、 化合物　　 D、 混合物

25、(12分)如图，已知抛物线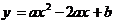与x轴交于A、B(3, 0)两点，与y轴交于点C，且OC＝3OA，设抛物线的顶点为D。

(1)求抛物线的解析式；

(2)在抛物线对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；

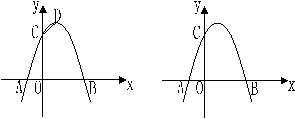(3)若平街于x轴的直线与该抛物线交于M、N两点(其中点M在点N的右侧)，在x轴上是否存在点Q，使△MNQ为等腰直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由。

24、(10分)在□ABCD中，BC＝2AB，M为AD的中点，设∠ABC＝α，过点C作直线AB的垂线，垂足为点E，连ME。

(1)如图①，当α＝90⁰，ME与MC的数量关系是　　　　　　　 ；∠AEM与∠DME的关系是　　　　　 。

(2)如图②，当60⁰＜α＜90⁰时，请问：(1)中的两个结论是否仍然成立？若成立，请证明；若不成立，请说明理由。

(3)如图③，当0⁰＜α＜60⁰时，请在图中画出图形，ME与MC的数量关系是　　　　　 ；∠AEM与∠DME的关系是　　　　　　　　　 。(直接写出结论即可，不必证明)

　　　　　　 图①　　　　　　　 图②　　　　　　　 图③

23、(10分)一家用电器开发公司研制出一种新型电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件，为了增加销量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件。

(1)求出月销售利润w(万元)(利润＝售价－成本价)与销售单价x(元)之间的函数关系式。

(2)为获得最大销售利润，每件产品的售价应为多少元？此时，最大月销售利润是多少？

(3)请你通过(1)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围，使月销售利润不低于480万元。

22、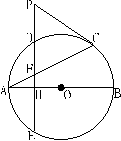(8分)如图：AB、AC分别是☉0的直径和弦，D为弧AC上一点，DE⊥AB于点H，交☉0于点E，交AC于点F。P为ED延长线上一点，连PC。

(1)若PC与☉0相切，判断△PCF的形状，并证明。

(2)若D为弧AC的中点，且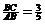，DH＝8，求☉0的半径。