1、空间中n(n≥3)个平面，其中任意三个平面无公垂面．那么，下面四个结论

(1)　　 没有任何两个平面互相平行；

(2)　　 没有任何三个平面相交于一条直线；

(3)　　 平面间的任意两条交线都不平行；

(4)　　 平面间的每一条交线均与n-2个平面相交．

其中，正确的个数为

(A)1　　　　　　　　 (B)2　　　　　　　 (C)3　　　　　　　 (D)4

有2002名运动员，号码依次为1，2，3，…，2002．从中选出若干名运动员参加仪仗队，但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积．那么被选为仪仗队的运动员至少能有多少人？给出你的选取方案，并简述理由．

已知x₀＝1，x₁＝3，x_n+1＝6x_n－x_n-1(n∈N₊)．

求证：数列{x_n}中无完全平方数．

已知△ABC的外角∠EAC平分线与△ABC的外接圆交于D，以CD为直径的圆分别交BC、CA于点P、Q．

求证：线段PQ平分△ABC的周长．

设正系数一元二次方程ax²+bx+c＝0有实根．证明：

(1)　　 max{a,b,c}≥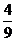(a+b+c)；

(2)　　 min{a,b,c}≤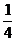(a+b+c)．

第二试

在三棱锥D-ABC中，AD＝a，BD＝b，AB＝CD＝c，且∠DAB+∠BAC+∠DAC＝180°，∠DBA+∠ABC+∠DBC＝180°．求异面直线AD与BC所成的角．

△ABC的三边长a、b、c(a≤b≤c)同时满足下列三个条件

(i)a、b、c均为整数；

(ii)a、b、c依次成等比数列；

(iii)a与c中至少有一个等于100．

求出(a,b,c­­)的所有可能的解．

6、同底的两个正三棱锥内接于同一个球．已知两个正三棱锥的底面边长为a，球的半径为R．设两个正三棱锥的侧面与底面所成的角分别为a、b，则tan(a+b)的值是　　　　　 ．

5、已知点(a,b)在曲线arcsinx＝arccosy上运动，且椭圆ax²+by²＝1在圆x²+y²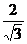＝的外部(包括二者相切的情形)．那么，arcsinb的取值范围是　　　　　 ．

4、银行计划将某项资金的40%给项目M投资一年，其余的60%给项目N．预计项目M有可能获得19%到24%的年利润，N有可能获得29%到34%的年利润．年终银行必须回笼资金，同时按一定的回扣率支付给储户．为使银行的年利润不少于给M、N总投资的10%而不大于总投资的15%，则给储户的回扣率的最小值是　　　　 ．