
非负实数x、y、z满足x2+y2+z2=1.
求证:1≤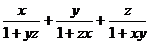 ≤
≤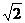 .
.
设C(I)是以△ABC的内心I为圆心的一个圆,点D、E、F分别是从I出发垂直于边BC、CA和AB的直线C(I)的交点.
求证:AD、BE和CF三线共点.
n为正整数,r>0为实数.证明:方程xn+1+rxn-rn+1=0没有模为r的复数根.
第二试
经过点M(2,-1)作抛物线y2=x的四条弦PiQi(i=1,2,3,4),且P1、P2、P3、P4四点的纵坐标依次成等差数列.
求证: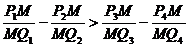 .
.
已知实数x、y满足x2+y2≤5.求f(x,y)=3|x+y|+|4y+9|+|7y-3x-18|的最大值与最小值.
6、使不等式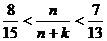 对惟一的一个整数k成立的最大正整数n为 .
对惟一的一个整数k成立的最大正整数n为 .
5、设a、b均为正数,且存在复数z满足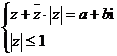 ,则ab的最大值等于
.
,则ab的最大值等于
.
4、从{1,2,3,…,20}中选出三个数,使得没有两个数相邻,有 种不同的选法.
3、在Rt△ABC中,AB=AC,以C为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AB内,且椭圆过A、B点,则这个椭圆的离心率等于 .
2、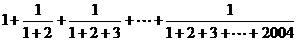 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com