1.(满分10分)某项选拔共有四轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考核，否则被淘汰。已知某选手能正确回答第一、二、三、四轮问题的概率分别为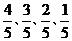，且各轮问题能否正确回答互不影响。

(1)求该选手进入第四轮才被淘汰的概率；　

　 (2)求该选手至多进入第三轮考核的概率。

实系数多项式f(x)=x³+ax²+bx+c满足b＜0，ab=9c．试判别此多项式是否有三个不同的实根，说明理由．

M是平面上所有点(x,y)的集合，其中x、y均是整数，且1≤x≤12，1≤y≤13．证明：不少于49个点的M的每一个子集，必包含一个矩形的4个顶点，且此矩形的边平行于坐标轴．

已知△ABC中，内心为I，外接圆为⊙O，点B关于⊙O的对径点为K，在AB的延长线上取点N，CB的延长线上取M，使得MC=NA=s，s为△ABC的半周长．证明：IK⊥MN．

　　　　　　　　　　 已知a、b、c∈R⁺，且a+b+c=1．

　　　　　　　　　　 证明：≤a²+b²+c²+4abc＜1．

第二试

数列{a_n}定义如下：a₁=3，a_n=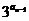(n≥2)．试求a_n(n≥2)的末位数．

　　　　　　　　　　 过正方体的某条对角线的截面面积为S，试求之值．

6、任给一个自然数k，一定存在整数n，使得xⁿ+x+1被x^k+x+1整除，则这样的有序实数对(n,k)是(对于给定的k)　　　　　　　 ．

5、已知集合{1,2,3,…,3n-1,3n}，可以分为n个互不相交的三元组{x,y,z}，其中x+y=3z，则满足上述要求的两个最小的正整数n是　　　　　　 ．

4、已知t＞0，关于x的方程为，则这个方程有相异实根的个数情况是　　　　　　　　　 ．