
(1)求 、
、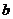 的值;
的值;
(2)若对 都有
都有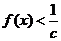 恒成立,求
恒成立,求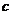 的取值范围.
的取值范围.
设公差为 ,
, ,
,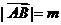 ,
, ,
,
由勾股定理可得: ,
,
解得 ,
, ,
,
 .
.
由倍角公式可得 ,解得
,解得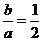 ,则离心率
,则离心率 .
.
(Ⅱ)直线 的方程为
的方程为 ,与双曲线方程
,与双曲线方程 联立,
联立,
将 ,
, 代入,化简有
代入,化简有 ,
,
又因为

利用根与系数的关系代入,有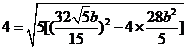 ,解得
,解得 .
.
故所求的双曲线方程为 .
.
且垂直于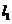 的直线
的直线 分别交
分别交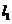 、
、 于
于 、
、 两点.已知
两点.已知 、
、 、
、 成等差数列,
成等差数列,
且 与
与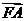 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设 被双曲线所截得的线段的长为
被双曲线所截得的线段的长为 ,求双曲线的方程.
,求双曲线的方程.
在矩形 中,
中, ,
,
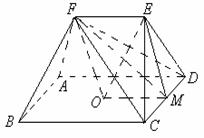 又
又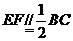 ,则
,则 ,连接
,连接 ,
,
于是四边形 为平行四边形.
为平行四边形.
∴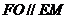 ,又∵
,又∵ 平面
平面 ,
,
且 平面
平面 ,∴
,∴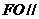 平面
平面 .
.
(2)连接 ,由(1)和已知条件,在等边
,由(1)和已知条件,在等边 中,
中,
 ,
, ,
, ,
,
所以 平面
平面 ,故
,故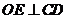 .
.
又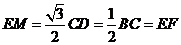 ,
,
因此平行四边形 为菱形,从而
为菱形,从而 ,
,
而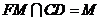 ,所以
,所以 平面
平面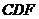 .
.
侧面 是等边三角形,棱
是等边三角形,棱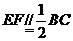 .
.
(1)证明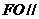 平面
平面 ;
;
(2)设 ,证明
,证明 平面
平面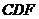 .
.

∴ ,
, ,
, ,
,
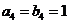 ,
, ,
, ,...
,...
假设 时,有
时,有 ,
,
则当 时,
时,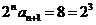 ,
,
从而 ,故数列
,故数列 的通项公式为
的通项公式为 .
.
又∵数列 是等差数列,∴公差
是等差数列,∴公差 ,
,
∴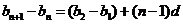
 ,
,

∴ .
.
(2)不存在 ,使得
,使得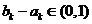 .
.
∵
 .
.
当 时,
时,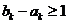 ,当
,当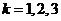 时,
时, ,
,
故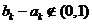 .
.
且 对任意的
对任意的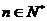 都成立,
都成立,
数列 是等差数列.
是等差数列.
(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)是否存在 ,使得
,使得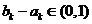 ?请说明理由.
?请说明理由.
两人同时取得黄球的概率为 ;
;
两人同时取得白球的概率为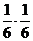 ;
;
故甲取胜的概率为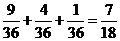 .
.
(2)用 表示甲的得分,则
表示甲的得分,则 的分布如下:
的分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
 |
 |
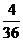 |
 |
所以,甲得分的期望 .
.
两人各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜.
(1)求甲取胜的概率;
(2)若又规定:当甲取红、黄、白球而胜的得分分别为 、
、 、
、 分,否则得
分,否则得 分,
分,
求甲得分的期望.
2.解:(1)由余弦定理,

 ,所以
,所以 .
.
(2)由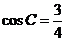 和
和 ,得
,得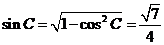 ,
,
由正弦定理得 ,解得
,解得 ,
,
由题设可得 ,
,
故

 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com