BCADC　 ACDBC

21．(本小题满分14分)已知圆C：.

(1)自点作圆C的切线,切点为M,求切线段AM的长．

(2)自点B(4,9)发出的光线m被y轴反射到x轴上后，再被x轴反射，若点C到此反射光线所在直线n的距离为6，求光线m所在直线的方程．

(3)从圆C外一点P(a，b)向圆引切线PT，T为切点，且|PT|=|PO| (O为原点)，求|PT|的最小值及此时P的坐标.

龙岩一中2009-2010学年第二学段(模块)考试

高一数学答案

20．(本小题满分14分)通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用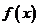表示学生掌握和接受概念的能力，x表示提出和讲授概念的时间(单位:分),可有以下的公式:

(1)开讲后多少分钟，学生的接受能力最强？能维持多长时间？　　　　　

(2)开讲后5分钟与开讲后20分钟比较，学生的接受能力何时强些？

(3)一道数学难题，需要55的接受能力以及13分钟时间，老师能否及时在学生一直达到所需接受能力的状态下讲授完这道难题？

19．(本小题满分13分)如图，平面PAD⊥平面ABCD，ABCD为正方形，∠PAD=90°，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点.

　 (1)求证：PB//平面EFG；

　 (2)求异面直线EG与BD所成的角的余弦值.

18. (本小题满分13分) 圆锥的底面半径为2cm，高为6cm.

(1)求它的体积；

(2)当它的内接圆柱的底面半径为何值时，圆锥的内接圆柱的全面积最大？最大值是多少？

17．(本小题满分13分)求过三点的圆的方程．

16．(本小题满分13分)已知三角形的三个顶点为，求边上的高所在的直线方程．

15. 对于任意实数k，直线与圆的位置关系是_______.

14. 设P为圆上的动点，则点P到直线的距离的最小值为_________.

13. 定义在[－2，2]上的偶函数时，单调递减，若则实数m的取值范围是　　　　　　　　 .