
18. 解:(1)ξ的可能取值为0,1,2 ……………… 1分
 ,
,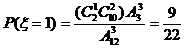
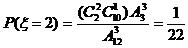 …… 4分
…… 4分
∴ξ的分布列为:
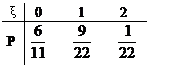 ……………… 6分
……………… 6分
∴ξ的数学期望为: 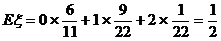 方差为:
方差为:
 …………… 8分
…………… 8分
(2)η的可能取值为1,2,3,且ξ+η=3
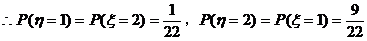
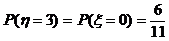 …… 10分
…… 10分
∴η的分布列为:
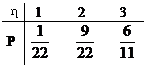 …… 12
…… 12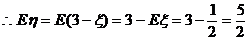
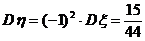 … 14分
… 14分
16. 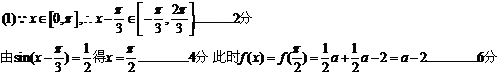
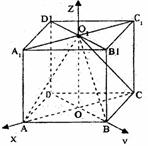
 17. (本小题满分12分) 解法一(1)过O作OF⊥BC于F,连接O1F,
17. (本小题满分12分) 解法一(1)过O作OF⊥BC于F,连接O1F,
∵OO1⊥面AC,∴BC⊥O1F,∴∠O1FO是二面角O1-BC-D的平面角,…3分
∵OB=2,∠OBF=60°,∴OF=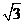 .在Rt△O1OF在,tan∠O1FO=
.在Rt△O1OF在,tan∠O1FO=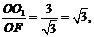
∴∠O1FO=60° 即二面角O1-BC-D为60° ………………6分
(2)在△O1AC中,OE是△O1AC的中位线,∴OE∥O1C
 ∴OE∥O1BC,∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F.
∴OE∥O1BC,∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F.
过O作OH⊥O1F于H,则OH是点O到面O1BC的距离,………………10分
∴OH=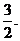 ∴点E到面O1BC的距离等于
∴点E到面O1BC的距离等于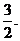 ………………12分
………………12分
解法二:(1)∵OO1⊥平面AC,∴OO1⊥OA,OO1⊥OB,又OA⊥OB,………2分
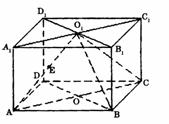
建立如图所示的空间直角坐标系(如图)
∵底面ABCD是边长为4,∠DAB=60°的菱形,∴OA=2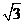 ,OB=2,
,OB=2,
则A(2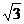 ,0,0),B(0,2,0),C(-2
,0,0),B(0,2,0),C(-2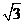 ,0,0),O1(0,0,3)……… 3分
,0,0),O1(0,0,3)……… 3分
设平面O1BC的法向量为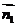 =(x,y,z),则
=(x,y,z),则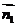 ⊥
⊥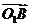 ,
,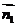 ⊥
⊥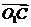 ,
,
∴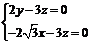 ,则z=2,则x=-
,则z=2,则x=-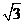 ,y=3,
,y=3,
∴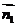 =(-
=(-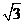 ,3,2),而平面AC的法向量
,3,2),而平面AC的法向量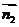 =(0,0,3)…………
5分
=(0,0,3)…………
5分
∴cos<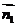 ,
,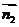 >=
>= ,设O1-BC-D的平面角为α, ∴cosα=
,设O1-BC-D的平面角为α, ∴cosα=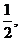 ∴α=60°.故二面角O1-BC-D为60°. …… 6分
∴α=60°.故二面角O1-BC-D为60°. …… 6分
(2)设点E到平面O1BC的距离为d, ∵E是O1A的中点,∴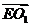 =(-
=(-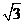 ,0,
,0,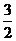 ),…… 9分
),…… 9分
则d=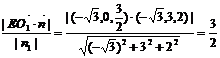 ∴点E到面O1BC的距离等于
∴点E到面O1BC的距离等于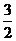 。…………… 12分
。…………… 12分
16解:
17解:
18解:
19解:
20解:
21解:
深圳市高级中学高三数学周练试题(综合试题 028) (2010-3-16)
1-8:BDBDA,CDB; 9. 充分不必要 10. ①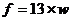 (2分); ②
(2分); ②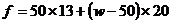 (3分)
(3分)
11. 4 12. 252 13. 2 14. 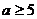 15.
15. 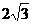
12、 。 13、 。 14、 。 15、 。
9、 。10、① 。② 。11、 。
21.(本小题满分14分)
已知函数 且任意的
且任意的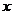 、
、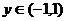 都有
都有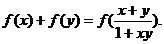
(1)若数列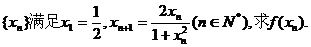
(2)求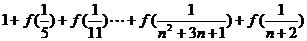 的值.
的值.
深圳市高级中学高三数学周练试题(综合试题 028) (2010-3-16)
姓名 学号 得分 .
20.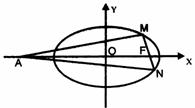 (本小题满分14分)已知椭圆
(本小题满分14分)已知椭圆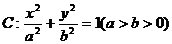 的离心率为
的离心率为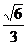 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且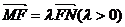 ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当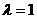 时,
时,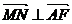 ;
;
(2)若当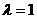 时有
时有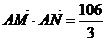 ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当 的值为6
的值为6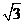 时, 求出直线MN的方程.
时, 求出直线MN的方程.
19.(本小题满分14分)
设函数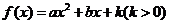 在
在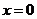 处取得极值,且曲线
处取得极值,且曲线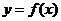 在点
在点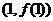 处的切线垂直于直线
处的切线垂直于直线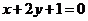 .
.
(Ⅰ)求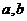 的值;
的值;
(Ⅱ)若函数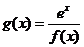 ,讨论
,讨论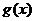 的单调性.
的单调性. 

18.(本小题满分14分)
在12个同类型的零件中有2个次品,抽取3次进行检验,每次任取一个,
并且取出不再放回,若以ξ和η分别表示取出次品和正品的个数
(1)求ξ的分布列,期望值及方差;
(2)求η的分布列,期望值及方差。
17.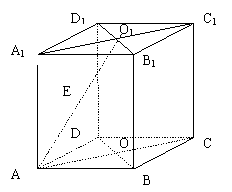 (本小题满分12分)
(本小题满分12分)
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°
的菱形,AC∩BD=O,A1C1∩B1D1=O1,E是O1A的中点
(1)求二面角O1-BC-D的大小;
(2)求点E到平面O1BC的距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com