23．下列叙述正确的是

A．c(NH₄⁺)相等的(NH₄)₂SO₄、(NH₄)₂Fe(SO₄)₂和NH₄Cl溶液中，溶质浓度大小关系是：c[(NH₄)₂Fe(SO₄)₂] ＜ c[(NH₄)₂SO₄] ＜ c(NH₄Cl)

B．无色透明的酸性溶液中，Cu²⁺、K⁺、SO₄^2－、NO₃^－ 能大量共存

C．0.2mol·L^－1 HCl溶液与等体积0.05 mol·L^－1 Ba(OH)₂溶液混合后，溶液的pH＝1

D．NaHCO₃溶液中：c(H⁺) + c(H₂CO₃)＝c(CO₃^2－) + c(OH^－)

22．高铁电池的总反应为：3Zn + 2K₂FeO₄ + 8H₂O　　　 3Zn(OH)₂ + 2Fe(OH)₃ + 4KOH

下列叙述错误的是

A．放电时每转移6mol电子，负极有2mol K₂FeO₄被还原

B．充电时阴极反应为：Zn(OH)₂ + 2e^- = Zn + 2OH^-

C．放电时正极反应为：FeO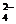+ 3e^- + 4H₂O = Fe(OH)₃ + 5OH^-

D．充电时阳极附近溶液的碱性增强

12．下列叙述正确的是　

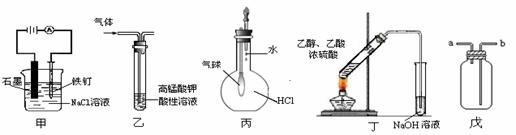
①装置甲可防止铁钉生锈　　　　　　　　　 ②装置乙可除去乙烯中混有的乙炔

③装置丙可验证HCl气体在水中的溶解性　　 ④装置丁可用于实验室制取乙酸乙酯

⑤装置戊可用于收集H₂、CO₂、Cl₂、HCl、NO₂等气体

A．①③⑤　　　　　 B．③④　　　　 C．①②④　　　　　 D．③⑤

11．下列离子方程式正确的是

A．石灰石溶于醋酸： CaCO₃ + 2CH₃COOH = 2CH₃COO^－+ Ca²⁺ + CO₂↑+ H₂O

B．钠与硫酸铜溶液反应: Cu²⁺ + 2Na = 2Na⁺ + Cu

C．铁屑溶于过量稀硝酸：3Fe + 8H⁺ + 2NO₃^－＝3Fe²⁺ + 2NO↑+ 4H₂O

D．FeI₂溶液中通入少量氯气：2Fe²⁺ + Cl₂＝ 2Fe³⁺ + 2Cl^－

10．A、B、C、D、E 五种短周期元素，核电荷数依次增加。只有D为金属，A 与D 同主族，C与E同主族，B 原子最外层电子数是内层电子数的2 倍，D⁺与C^3－具有相同的电子层结构。下列说法正确的是

A．C的氧化物都能跟碱反应

B．B的最高价氧化物的水化物是非电解质

C．C的氢化物与C的最高价氧化物的水化物能发生化合反应

D．沸点：CA₃＞EA₃　 离子半径：D⁺＞C ^3－

9．下列说法正确的是

A．乙烯和聚乙烯都能使溴的四氯化碳溶液褪色

B．淀粉和纤维素都可作为工业生产葡萄糖的原料

C．用水可区分乙酸乙酯和苯

D．钠跟乙醇反应比跟水反应剧烈

8．N_A为阿伏加德罗常数，下列叙述正确的是[M(Fe)=56]

A．常温下，pH=1的醋酸溶液中，醋酸分子的数目一定大于0.1N_A

B．22.4LCH₄和CH₃Cl的混合物所含有的分子数目为N_A

C．5.6 g铁粉在0.1mol氯气中充分燃烧，失去的电子数为0.3N_A

D．1mol过氧化氢分子中共用电子对数为3N_A

7．我国研制的新型“连续纤维增韧”航空材料宇航服，其主要成分由碳化硅、陶瓷和碳纤维复合而成，下列叙述正确的是

A．它耐高温，抗氧化　　　　　　　　　 B．它比钢铁轻、硬，但质地较脆

C．它有固定的熔、沸点　　　　　　　　 D．它是一种新型有机高分子材料

(18) 本题主要考查三角函数恒等变换及图象的对称性等基础知识, 同时考查运算求解能力。满分14分。

(Ⅰ) 解：因为f (x) 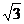＝sin2x－cos2x

　　　　　　　 　　＝ 2sin(2x－) ,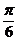

　　　 所以f (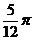) ＝ 2sin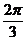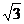＝.　　　　　　 ……………………(7分)

(Ⅱ) 解: 令2x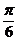－= k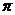+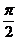(k∈Z), 得

x=,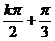

所以函数f (x)图象的对称轴方程是x=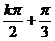(k∈Z).　 ……………(14分)

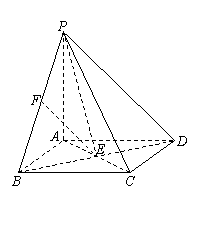(19) 本题主要考查空间线线、线面、面面位置关系, 线面角大小计算, 同时考查空间想象能力和推理论证能力。满分14分。

　(Ⅰ)　 证明: 如图, 连结BD, 则E是BD的中点.

又F是PB的中点,

所以EF∥PD.

　 因为EF不在平面PCD内,

所以EF∥平面PCD.　　　　 …………………(6分)

(Ⅱ)　 解: 连结PE.

因为ABCD是正方形，

所以BD⊥AC.

又PA⊥平面ABC，

所以PA⊥BD.

因此BD⊥平面PAC.

故∠EPD是PD与平面PAC所成的角.

因为EF∥PD,

所以EF与平面PAC所成的角的大小等于∠EPD.

因为PA＝AB＝AD, ∠PAD＝∠BAD＝,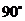

所以Rt△PAD ≌ Rt△BAD.

因此PD＝BD.

在Rt△PED中,

　　　　 sin∠EPD＝,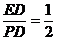

　　　　 ∠EPD=.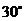

所以EF与平面PAC所成角的大小是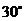.　　　 …………………(14分)

(20) 本题主要考查数列递推关系，等比数列的定义，求和公式等基础知识，同时考查运算求解能力。满分14分。

(Ⅰ)　 解: 由 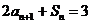, 得

,

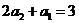又,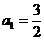

所以.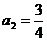

由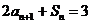, (n≥2)相减, 得

　　　 ,

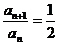又 ,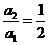

所以数列{a_n}是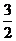以为首项，以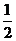为公比的等比数列.

因此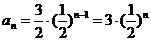( n∈N^*).　　　　 …………………(7分)

(Ⅱ)　 解: 由题意与(Ⅰ), 得

　,

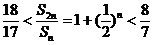即　 　.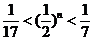

因为　 　, ,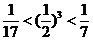

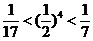所以n的值为3, 4.　　　　　　　　　　　　　 …………………(14分)

(21) 本题主要考查函数的单调性、最值等基本性质、导数的应用等基础知识, 同时考查抽象概括能力和运算求解能力。

(Ⅰ)　 解: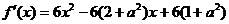　

,

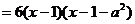　　　　　　 因为函数f (x)在R上单调,

所以 ,

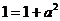即a = 0.　　　　　　　　　　　　　　　　　 …………………(6分)

(Ⅱ)　 解: 因为,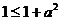

所以 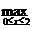{f (x)}= max{ f (1) , 　f (2)}= max{3a²+3, 5}=5,

即 3a²+3 ≤ 5,

解此不等式, 得

　,

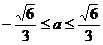所以a的取值范围是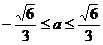.　　　　 …………………(15分)

(22) 本题主要考查抛物线的几何性质，直线与抛物线的位置关系等基础知识，考查解析几何的基本思想方法和综合解题能力。满分15分。

(Ⅰ)　 解: 设抛物线C的方程是x² = ay,

则,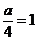

即a = 4 .

故所求抛物线C的方程为x² = 4y .　　　　　　 …………………(5分)

(Ⅱ) 解:设P(x₁, y₁), Q(x₂, y₂) ,

则抛物线C在点P处的切线方程是

,

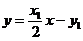直线PQ的方程是

.

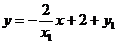将上式代入抛物线C的方程, 得

,

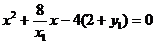故 x₁+x₂=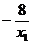, x₁x₂=－8－4y₁,

所以 x₂=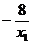－x₁ , y₂=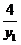+y₁+4 .

而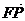＝(x₁, y₁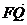－1), ＝(x₂, y₂－1),

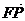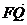×＝x₁ x₂+(y₁－1) (y₂－1)

＝x₁ x₂+y₁ y₂－(y₁+y₂)+1

＝－4(2+y₁)+ y₁(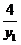+y₁+4)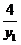－(+2y₁+4)+1

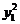＝－2y₁ 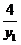－－7

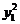＝(+2y₁+1)－4(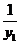+y₁+2)

＝(y₁+1)²－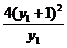

＝

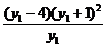
＝0,

故 y₁＝4, 此时, 点P的坐标是(±4,4) .

经检验, 符合题意.

所以, 满足条件的点P存在, 其坐标为P(±4,4). ………………(15分)

(11) 0　 　(12) 过原点的平面(原点，平面每对一个得2分)　　　　 (13) 1　　　

(14) 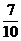　　　　　　(15) 1　　　　　　 (16) 169　　　　　　　　　　　 (17) (－∞,2]