
4、甲植株(基因型Aa)的枝条嫁接到乙植株(基因型aa)茎上形成新的植株,该新植株自花传粉后又产生了新植株,两次新植株形成的生殖方式及新植株基因型分别是
A、都是有性生殖方式,两次形成的新植株的基因型都是Aa
B、第一次形成新植株是无性生殖,第二次形成新植株是有性生殖,两次形成的新的基因型前者为Aa、aa,后者是AA、Aa、aa。
C、都是有性生殖方式,两次形成的新植株,基因型都是AA、Aa、aa
D、第一次形成的新植株是无性生殖,第二次形成的新植株是有性生殖,两次形成的新的基因型,前者是Aa,后者是AA、Aa、aa
3、菊花的紫色和白色性状由一对等位基因控制的,紫色(R)对白色(r)显性,现已克隆到控制紫色的基因R,如果你打算利用上述材料开展研究,那么下表选项中不合理的是
|
选项 |
实验方案 |
实验目的 |
|
A |
白花植物×紫花植物 |
判断基因型 |
|
B |
将控制开紫花的基因转入其他植物中 |
改变受体植物花的颜色 |
|
C |
将R基因转入大肠杆菌,并大量表达紫色蛋白 |
生产紫色蛋白作饲料 |
|
D |
用紫花纯合子的嫩芽用组织培养获得纯合子植株 |
无性繁殖 |
2、某人群中常染色体显性遗传病的发病率为36%,一对夫妇中丈夫患病,妻子正常,他们所生的子女患该病的概率是
A、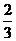 B、
B、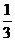 C、
C、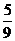 D、
D、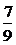
1、三类营养物质氧化时释放能量与耗氧量如下表:
|
营养物质 |
体外燃烧释放能量 (kj/g) |
体内氧化分解释放能量 (kj/g) |
耗氧量 (dl/g) |
|
糖 |
17 |
17 |
0.83 |
|
蛋白质 |
23.5 |
18 |
0.95 |
|
脂肪 |
39.8 |
39.8 |
2.03 |
根据表中内容不能作出的判断是
A、糖是生命活动的主要能源物质
B、同质量时,脂肪贮存能量最多
C、体内蛋白质分解释放能量的差异可能是因为分解产物不完全相同
D、耗氧量的多少可能与它们含有元素比例不同有关
6.正态分布密度函数: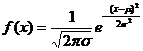 ,(σ>0,-∞<x<∞),其中x是随机变量的取值,μ为正态分布的均值,σ是正态分布的标准差.正态分布一般记为
,(σ>0,-∞<x<∞),其中x是随机变量的取值,μ为正态分布的均值,σ是正态分布的标准差.正态分布一般记为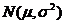 ;正态曲线的性质:(1)曲线在x轴的上方,与x轴不相交 ,(2)曲线关于直线x=μ对称 ,(3)当x=μ时,曲线位于最高点
;正态曲线的性质:(1)曲线在x轴的上方,与x轴不相交 ,(2)曲线关于直线x=μ对称 ,(3)当x=μ时,曲线位于最高点  (4)当x<μ时,曲线上升(增函数);当x>μ时,曲线下降(减函数),并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近 ,(5)μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,总体分布越分散;σ越小,曲线越“高”.总体分布越集中。当μ=0、σ=l时,正态总体称为标准正态总体,其相应的函数表示式是
(4)当x<μ时,曲线上升(增函数);当x>μ时,曲线下降(减函数),并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近 ,(5)μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,总体分布越分散;σ越小,曲线越“高”.总体分布越集中。当μ=0、σ=l时,正态总体称为标准正态总体,其相应的函数表示式是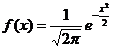 ,(-∞<x<+∞)。对于标准正态总体
,(-∞<x<+∞)。对于标准正态总体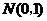 ,
,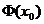 表示总体取值小于
表示总体取值小于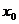 的概率, 即
的概率, 即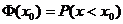 ,(
,(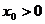 );当
);当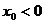 时,
时,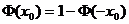 ;而当
;而当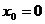 时,
时,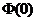 =0.5;计算正态总体的概率应结合正态曲线(面积)进行。
=0.5;计算正态总体的概率应结合正态曲线(面积)进行。
[举例1]设随机变量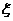 服从标准正态分布
服从标准正态分布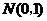 ,已知
,已知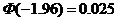 ,则
,则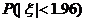 =( ) (07高考湖南理5)
=( ) (07高考湖南理5)
A.0.025 B.0.050 C.0.950 D.0.975
解析: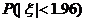 =
=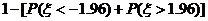 ,因为标准正态曲线关于y轴对称,
,因为标准正态曲线关于y轴对称,
所以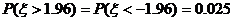 ,故
,故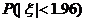 =0.950,选C。
=0.950,选C。
[举例2]以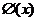 表示标准正态总体在区间
表示标准正态总体在区间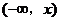 内取值的概率,若随机变量
内取值的概率,若随机变量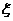 服从正态分布
服从正态分布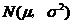 ,则概率
,则概率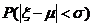 等于( B )(07高考安徽理10)
等于( B )(07高考安徽理10)
A.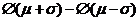 B.
B.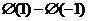
C.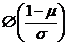 D.
D.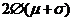
解析: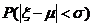 即正态分布
即正态分布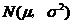 的分布曲线与直线
的分布曲线与直线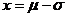 、
、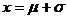 、
、
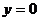 所围成的区域面积,也就是标准正态分布
所围成的区域面积,也就是标准正态分布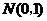 的分布曲线与直线
的分布曲线与直线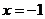 、
、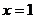 、
、
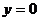 所围成的区域面积,即
所围成的区域面积,即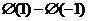 ,故选B。
,故选B。
[巩固1]在某项测量中,测量结果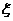 服从正态分布
服从正态分布 .若
.若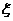 在
在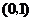 内取值的概率为0.4,则
内取值的概率为0.4,则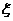 在
在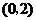 内取值的概率为
.(07高考全国卷Ⅱ理14)
内取值的概率为
.(07高考全国卷Ⅱ理14)
[巩固2]已知随机变量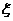 服从正态分布
服从正态分布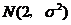 ,
,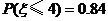 ,则
,则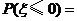 ( )
( )
A.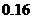 B.
B.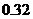 C.
C.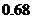 D.
D.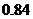 (07高考浙江理5)
(07高考浙江理5)
5.熟悉方差的计算公式和性质,如:样本同加(减)一个常数,方差不变;样本同乘一个常数k, 方差变为原来的k2倍;“标准差”是方差的算术平方根。样本的方差和标准差是反映其“稳定性”的量。对于离散型随机变量ξ,如果它所有可能取的值是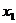 ,
,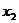 ,…,
,…,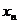 ,…,且取这些值的概率分别是
,…,且取这些值的概率分别是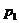 ,
,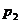 ,…,
,…,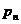 ,…,那么,
,…,那么,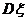 =
=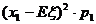 +
+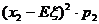 +…+
+…+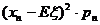 +…称为随机变量ξ的方差,式中的
+…称为随机变量ξ的方差,式中的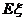 是随机变量ξ的期望.
是随机变量ξ的期望.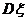 的算术平方根
的算术平方根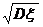 叫做随机变量ξ的标准差,记作
叫做随机变量ξ的标准差,记作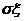 。
。
[举例]某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为
(A)1 (B)2 (C)3 (D)4
解析:由题意可得:x+y=20,(x-10)2+(y-10)2=8,解这个方程组需要用一些技巧,因为不要直接求出x、y,只要求出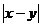 ,设x=10+t, y=10-t, 由(x-10)2+(y-10)2=8得t2=4;
,设x=10+t, y=10-t, 由(x-10)2+(y-10)2=8得t2=4;
∴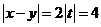 ,故选D。
,故选D。
[巩固1]甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
|
甲的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
5 |
5 |
5 |
5 |
|
乙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
6 |
4 |
4 |
6 |
|
丙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
4 |
6 |
6 |
4 |
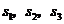 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
A.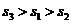 B.
B.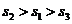
C. D.
D.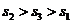 ( 07高考宁夏理 11)
( 07高考宁夏理 11)
[巩固2]随机变量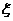 的分布列如下:
的分布列如下:
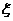
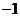
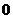
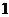
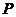
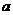
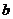
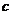
其中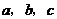 成等差数列,若
成等差数列,若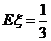 ,则
,则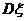 的值是
.(07高考浙江理15)
的值是
.(07高考浙江理15)
4.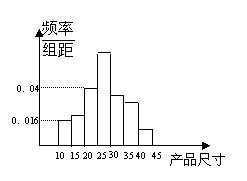 “读懂”样本频率分布直方图:直方图的高=
“读懂”样本频率分布直方图:直方图的高= ,直方图中小矩形框的面积是频率;频率×样本个数=频数。
,直方图中小矩形框的面积是频率;频率×样本个数=频数。
[举例1]从一条生产线上每隔30分钟取一件产品,共
取了n件,测得其尺寸后,画得其频率分布直方图如右,
尺寸在[15,45]内的频数为46,则尺寸在[20,25]内
的产品个数为
解析:由直方图可见,尺寸在[15,45]内的频率为
1-0.016×5=0.92, ∴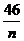 =0.92,得n=50;
=0.92,得n=50;
|
分组 |
频数 |
 |
 |
 |
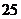 |
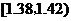 |
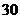 |
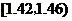 |
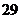 |
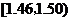 |
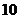 |
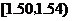 |
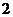 |
|
合计 |
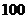 |
而尺寸在[20,25]内的频率为0.04×5=0.2,
∴尺寸在[20,25]内的产品个数为:0.2×50=10.
[巩固1] 在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
(I)画出该产品纤度的频率分布直方图;
(II)估计纤度落在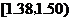 中的概率及纤度小于
中的概率及纤度小于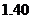 的概率是多少?
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值是
的中点值是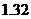 )作为代表.据此,估计纤度的期望.
)作为代表.据此,估计纤度的期望.
[巩固2]一个社会调查机构
就某地居民的月收入调查了
10 000人,并根据所得数据
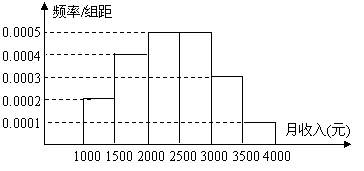 画了样本的频率分布直方图
画了样本的频率分布直方图
(如右图).为了分析居民的
收入与年龄、学历、职业等
方面的关系,要从这10 000
人中再用分层抽样方法抽出
100人作进一步调查,则在
[2500,3000)(元)月收入
段应抽出 人.
3.随机抽样需借助于随机数表(先对总体逐一编号),分层抽样的关键是“按比例”:总体中各层的比例等于样本中各层的比例。在所有的抽样中,每一个个体被抽到的概率相等。
[举例]从2004名学生中选取50名组成参观团,若采用下面的方法选取: 先用简单随机抽样
从2004人中剔除4人,剩下的2000人再按系统抽样的方法进行.则每人入选的概率( )
A、不全相等 B、均不相等
C、都相等,且为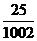 D、都相等,且为
D、都相等,且为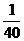
解析:某人“入选”,首先在第一步的随机抽样中要不被剔除,其概率为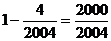 ,
,
在第二步的系统抽样中被抽中的概率为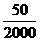 ,故每人入选的概率为
,故每人入选的概率为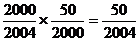
[巩固]
某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:5。现用分层抽样方法抽出一个容量为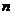 的样本,样本中A种型号产品有16件。那么此样本的容量n= 。
的样本,样本中A种型号产品有16件。那么此样本的容量n= 。
2.如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率是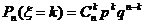 ,(k=0,1,2,…,n,
,(k=0,1,2,…,n,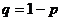 ).称这样的随机变量ξ服从二项分布,记作ξ-B(n,p),其中n,p为参数;若ξ-B(n,p),则
).称这样的随机变量ξ服从二项分布,记作ξ-B(n,p),其中n,p为参数;若ξ-B(n,p),则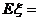 np.
np.
[举例]某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为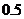 ,
,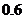 ,
,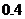 ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为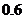 ,
,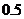 ,
,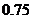 .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为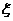 ,求随机变量
,求随机变量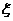 的期望.
的期望.
(07高考江西理19)
解析:分别记甲、乙、丙经第一次烧制后合格为事件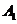 ,
, ,
,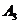 ,
,
(1)设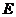 表示第一次烧制后恰好有一件合格,则
表示第一次烧制后恰好有一件合格,则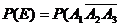 )+
)+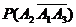 +
+
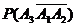
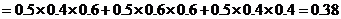 .
.
(2)解法一:分别记甲、乙、丙经过两次烧制后合格为事件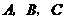 ,则
,则
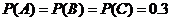 ,所以
,所以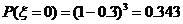 ,
,
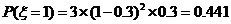 ,
,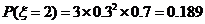 ,
,
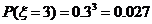 .于是,
.于是,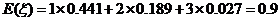
解法二:因为每件工艺品经过两次烧制后合格的概率均为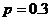 ,
,
所以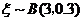 ,故
,故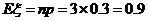 .
.
[巩固] 一个袋中装有3个红球,7个白球,从袋中随机摸出一个球,记录颜色后放回,连摸5次,试求摸到红球的次数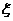 的分布列及期望
的分布列及期望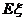 。
。
1.离散型随机变量ξ取每一个值xi(i=1,2,…)的概率为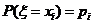 ,则P1+P2+…=1;
,则P1+P2+…=1;
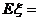
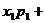
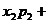 …
…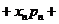 … 为ξ的数学期望,期望是反映随机变量“均值”的量,
… 为ξ的数学期望,期望是反映随机变量“均值”的量,
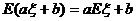 ;求离散型随机变量ξ的期望的基本步骤:①理解ξ的意义,写出ξ可能取的全部值;②求ξ取各个值的概率,写出分布列;③根据分布列,由期望的定义求出Eξ
;求离散型随机变量ξ的期望的基本步骤:①理解ξ的意义,写出ξ可能取的全部值;②求ξ取各个值的概率,写出分布列;③根据分布列,由期望的定义求出Eξ 
[举例] 设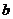 和
和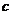 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量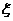 表示方程
表示方程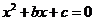 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程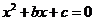 有实根的概率;(Ⅱ)求
有实根的概率;(Ⅱ)求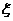 的分布列和数学期望;
的分布列和数学期望;
解析:(Ⅰ)由题意知:设基本事件空间为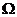 ,记“方程
,记“方程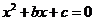 没有实根”为事件
没有实根”为事件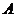 ,“方程
,“方程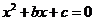 有且仅有一个实根”为事件
有且仅有一个实根”为事件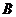 ,“方程
,“方程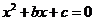 有两个相异实数”为事件
有两个相异实数”为事件 ,则
,则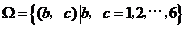 ,
,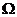 是的基本事件总数为36个,
是的基本事件总数为36个,
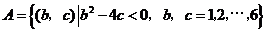 ,
,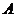 中的基本事件总数为17个;
中的基本事件总数为17个;
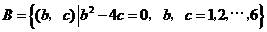 ,
,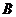 中的基本事件总数为
中的基本事件总数为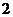 个;
个;
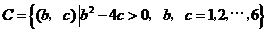 ,
, 中的基本事件总数为17个;
中的基本事件总数为17个;
又因为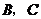 是互斥事件,故所求概率
是互斥事件,故所求概率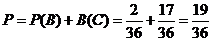 .
.
(Ⅱ)由题意,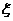 的可能取值为
的可能取值为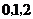 ,则
,则
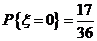 ,
,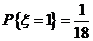 ,
,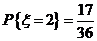 ,
,
故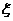 的分布列为:
的分布列为:
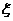
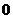
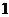
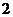
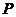
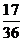
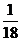
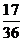
所以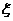 的数学期望
的数学期望 。
。
[巩固]某商场经销某商品,根据以往资料统计,顾客采用的付款期数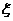 的分布列为
的分布列为
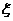 |
1 |
2 |
3 |
4 |
5 |
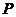 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.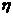 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件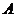 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率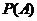 ;
;
(Ⅱ)求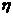 的分布列及期望
的分布列及期望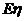 .(07高考全国卷(Ⅰ)理18)
.(07高考全国卷(Ⅰ)理18)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com