
11.已知函数 y=sin(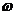 x+
x+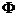 )与直线y=
)与直线y= 的交点中距离最近的两点距离为
的交点中距离最近的两点距离为 ,那么此函数的周期是( )
,那么此函数的周期是( )
A  B
B 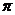 C 2
C 2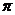 D 4
D 4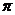
正确答案:B
错因:不会利用范围快速解题。
10. 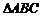 中,
中,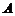 、
、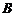 、C对应边分别为
、C对应边分别为 、
、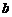 、
、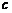 .若
.若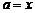 ,
,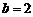 ,
,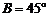 ,且此三角形有两解,则
,且此三角形有两解,则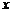 的取值范围为 ( )
的取值范围为 ( )
A.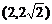 B.
B.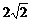 C.
C.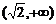 D.
D. 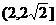
正确答案:A
错因:不知利用数形结合寻找突破口。
9. 在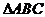 中,
中,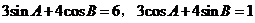 ,则
,则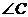 的大小为( )
的大小为( )
A. 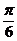 B.
B.
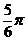 C.
C.
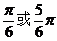 D.
D.
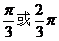
解:由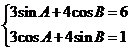 平方相加得
平方相加得
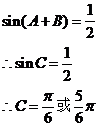
若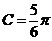
则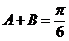
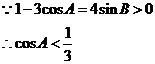 又
又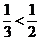
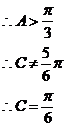
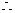 选A
选A
说明:此题极易错选为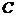 ,条件
,条件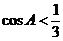 比较隐蔽,不易发现。这里提示我们要注意对题目条件的挖掘。
比较隐蔽,不易发现。这里提示我们要注意对题目条件的挖掘。
8. 若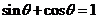 ,则对任意实数
,则对任意实数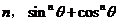 的取值为( )
的取值为( )
A. 1 B. 区间(0,1)
C. 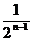 D.
不能确定
D.
不能确定
解一:设点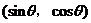 ,则此点满足
,则此点满足

解得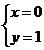 或
或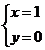
即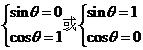
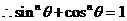
 选A
选A
解二:用赋值法,
令
同样有
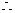 选A
选A
说明:此题极易认为答案A最不可能,怎么能会与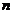 无关呢?其实这是我们忽略了一个隐含条件
无关呢?其实这是我们忽略了一个隐含条件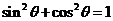 ,导致了错选为C或D。
,导致了错选为C或D。
7.已知tana tanb是方程x2+3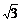 x+4=0的两根,若a,bÎ(-
x+4=0的两根,若a,bÎ(-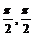 ),则a+b=( )
),则a+b=( )
A.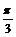 B.
B.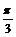 或-
或-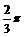 C.-
C.-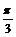 或
或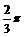 D.-
D.-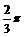
正确答案:D 错因:学生不能准确限制角的范围。
6. 在DABC中,2sinA+cosB=2,sinB+2cosA=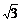 ,则ÐC的大小应为( )
,则ÐC的大小应为( )
A.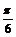 B.
B.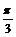 C.
C.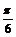 或
或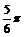 D.
D.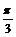 或
或
正确答案:A 错因:学生求ÐC有两解后不代入检验。
5.函数y=Asin(wx+j)(w>0,A¹0)的图象与函数y=Acos(wx+j)(w>0,
A¹0)的图象在区间(x0,x0+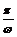 )上( )
)上( )
A.至少有两个交点 B.至多有两个交点
C.至多有一个交点 D.至少有一个交点
正确答案:C 错因:学生不能采用取特殊值和数形结合的思想方法来解题。
4.下列四个函数y=tan2x,y=cos2x,y=sin4x,y=cot(x+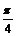 ),其中以点(
),其中以点(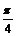 ,0)为中心对称的三角函数有( )个
,0)为中心对称的三角函数有( )个
A.1 B.2 C.3 D.4
正确答案:D 错因:学生对三角函数图象的对称性和平移变换未能熟练掌握。
3.曲线y=2sin(x+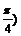 cos(x-
cos(x-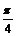 )和直线y=
)和直线y=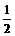 在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3……,则|P2P4|等于 ( )
在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3……,则|P2P4|等于 ( )
A.p B.2p C.3p D.4p
正确答案:A 错因:学生对该解析式不能变形,化简为Asin(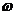 x+
x+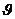 )的形式,从而借助函数图象和函数的周期性求出|P2P
)的形式,从而借助函数图象和函数的周期性求出|P2P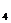 |。
|。
2.函数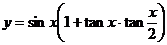 的最小正周期为
( )
的最小正周期为
( )
A 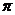 B
B 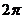 C
C 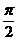 D
D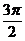
错误分析:将函数解析式化为 后得到周期
后得到周期 ,而忽视了定义域的限制,导致出错.
,而忽视了定义域的限制,导致出错.
答案: B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com