
5、已知函数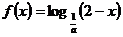 在其定义域上单调递减,则函数
在其定义域上单调递减,则函数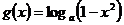 的单调减区间是( )
的单调减区间是( )
A. 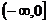 B.
B.
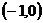 C.
C.
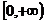 D.
D.
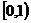
4、将函数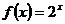 的图象向左平移一个单位得到图象
的图象向左平移一个单位得到图象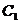 ,再将
,再将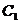 向上平移一个单位得图象
向上平移一个单位得图象 ,作出
,作出 关于直线
关于直线 对称的图象
对称的图象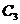 ,则
,则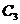 对应的函数的解析式为( )
对应的函数的解析式为( )
A. 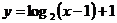 B.
B.
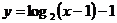
C. 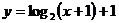 D.
D.
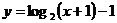
3、已知0<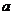 <1,
<1,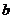 <-1,则函数
<-1,则函数 的图象必定不经过( )
的图象必定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2、已知函数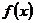 的定义域为[0,1],值域为[1,2],则函数
的定义域为[0,1],值域为[1,2],则函数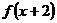 的定义域和值域分别是( )
的定义域和值域分别是( )
A. [0,1] ,[1,2] B. [2,3] ,[3,4]
C. [-2,-1] ,[1,2] D. [-1,2] ,[3,4]
1、已知函数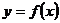 ,
,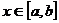 ,那么集合
,那么集合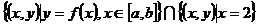 中元素的个数为( )
中元素的个数为( )
A. 1 B. 0 C. 1或0 D. 1或2
13.设a、b∈R,求证: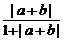 ≤
≤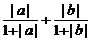
证明:当|a+b|=0时,不等式已成立
当|a+b|≠0时,∵ |a+b|≤|a|+|b|
∴ 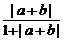 =
=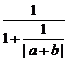 ≤
≤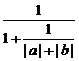 =
=
=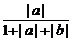 +
+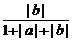 ≤
≤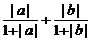
点评:错证:∵|a+b|≤|a|+|b|
∴ 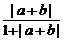 ≤
≤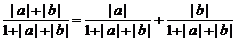 ≤
≤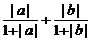 ①
①
错因:①的推理无根据。
12.在边长为a的正三角形中,点P、Q、R分别在BC、CA、AB上,且BP+CQ+AR=a,设BP=x,CQ=y,AR=z,三角形PQR的面积为s,求s的最大值及相应的x、y、z的值。
解 设ΔBPR、ΔPCR、ΔARQ的面积为s1、、s2、s3,则
S=SΔABC-S1-S2-S3=a2-[a2-(xy+xz+yz)]=(xy+xz+yz)
由x+y+z=a,得xy+yz+zx≤,∴Smav=a2,此时,x=y=z=
错因:不知如何使用基本不等式。
11.设集合M=[-1,1],N=[-,],f(x)=2x2+mx-1,若x∈N,m∈M,求证|f(x)|≤
证明:|f(x)|=|2x2+mx-1|= |(2x2-1)+mx|≤|(2x2-1)|+|mx|= (2x2-1)+|mx|≤(2x 2-1)+| x|
=-2(| x|-)2+≤
错因:不知何时使用绝对值不等式。
10. 设函数f(x)=logb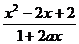 (b>0且b≠1),
(b>0且b≠1),
(1)求f(x)的定义域;
(2)当b>1时,求使f(x)>0的所有x的值。
解 (1)∵x2-2x+2恒正,
∴f(x)的定义域是1+2ax>0,
即当a=0时,f(x)定义域是全体实数。
当a>0时,f(x)的定义域是(-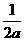 ,+∞)
,+∞)
当a<0时,f(x)的定义域是(-∞,-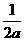 )
)
(2)当b>1时,在f(x)的定义域内,f(x)>0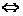
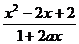 >1
>1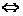 x2-2x+2>1+2ax
x2-2x+2>1+2ax
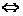 x2-2(1+a)x+1>0
x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
(i)当Δ<0时,即-2<a<0时
∵x2-2(1+a)x+1>0
∴f(x)>0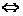 x<-
x<-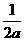
(ii)当Δ=0时,即a=-2或0时
若a=0,f(x)>0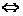 (x-1)2>0
(x-1)2>0
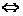 x∈R且x≠1
x∈R且x≠1
若a=-2,f(x)>0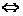 (x+1)2>0
(x+1)2>0
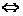 x<
x< 且x≠-1
且x≠-1
(iii)当△>0时,即a>0或a<-2时
方程x2-2(1+a)x+1=0的两根为
x1=1+a-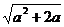 ,x2=1+a+
,x2=1+a+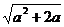
若a>0,则x2>x1>0>-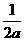
∴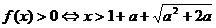 或
或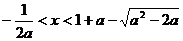
若a<-2,则
∴f(x)>0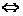 x<1+a-
x<1+a-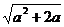 或1+a+
或1+a+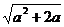 <x<-
<x<-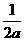
综上所述:当-2<a<0时,x的取值集合为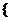 x|x<-
x|x<-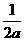
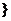
当a=0时,x∈R且x≠1,x∈R,当a=-2时: x|x<-1或-1<x<
x|x<-1或-1<x<
当a>0时,x∈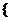 x|x>1+a+
x|x>1+a+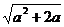 或-
或-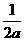 <x<1+a-
<x<1+a-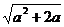
当a<-2时,x∈ x|x<1+a-
x|x<1+a-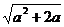 或1+a+
或1+a+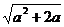 <x<-
<x<-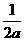
错误原因:解题时易忽视函数的定义域,不会合理分类。
9.方程 的两根都大于2,求实数
的两根都大于2,求实数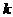 的取值范围。
的取值范围。
解:设方程的两根为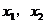 ,则必有
,则必有
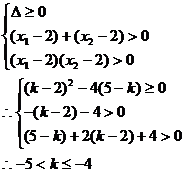
说明:此题易犯这样的错误:
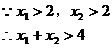
且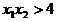
和判别式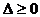 联立即得
联立即得 的范围
的范围
原因是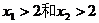 只是
只是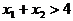 的充分条件
的充分条件
即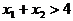 不能保证
不能保证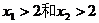 同时成立
同时成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com