
1.(石庄中学)设ABCD是空间四边形,E,F分别是AB,CD的中点,则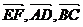 满足( )
满足( )
A 共线 B 共面 C 不共面 D 可作为空间基向量
正确答案:B 错因:学生把向量看为直线。
6.设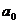 为常数,且
为常数,且
1)
证明对任意 ≥
≥ ;
;
2)
假设对任意n≥1有 ,求
,求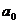 的取值范围
的取值范围
证明:①设
用 代入,解出:
代入,解出:
 是公比为-2,首项为
是公比为-2,首项为 的等比数列。
的等比数列。

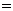
 ,
,
即
②若
 成立,特别取
成立,特别取 有
有



下面证明 时,对任意
时,对任意 ,有
,有
由 通项公式
通项公式
 ,
,
i)
当 时,
时,

ii) 当 时,
时,
 ≥0
≥0
故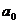 的取值范围为
的取值范围为
误解:①对于等比数列: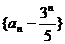 先构造出
先构造出 求
求 ,难度较大,若用数学归纳法证明同学容易想到。
,难度较大,若用数学归纳法证明同学容易想到。
②通过对n为奇数或为偶数的讨论找出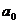 的取值范围有难度。
的取值范围有难度。
5.已知数列 中,a1=8, a4=2且满足
中,a1=8, a4=2且满足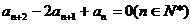 (1)求数列
(1)求数列 的
的
通项公式(2)设 ,求Sn
,求Sn
(3)设 ,是否存在最大的整数m,使得对任意
,是否存在最大的整数m,使得对任意 均有
均有 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。
答案:(1)
 (2)Sn=
(2)Sn= 

(3)由(1)可得

 由Tn为关于n的增函数,故
由Tn为关于n的增函数,故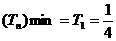 ,于是欲使
,于是欲使 对
对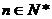 恒成立,则
恒成立,则 存在最大的整数m=7满足题意。
存在最大的整数m=7满足题意。
错因:对(2)中 表达式不知进行分类讨论;对(3)忽视讨论Tn的单调性。
表达式不知进行分类讨论;对(3)忽视讨论Tn的单调性。
4.学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A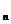 、B
、B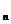 分别表示在第n个星期一选A、B菜的人数。(1)试以A
分别表示在第n个星期一选A、B菜的人数。(1)试以A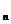 表示A
表示A ;(2)若A
;(2)若A =200,求{A
=200,求{A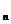 }的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
}的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
正确答案:(1)由题可知,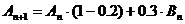 ,又
,又 ;
;
所以整理得: 。(2)若A
。(2)若A =200,且
=200,且 ,则设
,则设 则
则 ,
,
∴ 即{A
即{A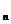 -600}可以看成是首项为-400,公比为
-600}可以看成是首项为-400,公比为 的等比数列。
的等比数列。
∴ ;(3)∵
;(3)∵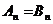 ,又
,又 则
则 , 由
, 由 得
得 。即第3个星期一时,选A与选B的人数相等。
。即第3个星期一时,选A与选B的人数相等。
错因:不会处理非等差非等比数列。
3.等比数列 的前
的前 项和为
项和为 ,求公比
,求公比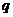 。
。
解:若
则

 矛盾
矛盾


说明:此题易忽略 的情况,在等比数列求和时要分公比
的情况,在等比数列求和时要分公比 两种情况进行讨论。
两种情况进行讨论。
2.已知正项数{an}满足a1= a (0<a<1) ,且
 ,求证:
,求证:
(I)  ;
(II)
;
(II)
 .
.
解析:(I) 将条件 变形,得
变形,得 .
.
于是,有 ,
, ,
, ,……
,…… .
.
将这n-1个不等式叠加,得 ,故
,故 .
.
(II) 注意到0<a<1,于是由(I)得 =
= ,
,
从而,有

 .
.
1.已知一个等比数列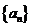 前四项之积为
前四项之积为 ,第二、三项的和为
,第二、三项的和为 ,求这个等比数列的公比.
,求这个等比数列的公比.
[错解] 四个数成等比数列,可设其分别为
四个数成等比数列,可设其分别为
则有 ,解得
,解得 或
或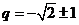 ,
,
故原数列的公比为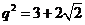 或
或
[错解分析]按上述设法,等比数列公比 ,各项一定同号,而原题中无此条件
,各项一定同号,而原题中无此条件
[正解]设四个数分别为
则 ,
,

由 时,可得
时,可得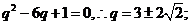
当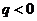 时,可得
时,可得
6.若数列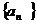 为等差数列且
为等差数列且 ,则数列
,则数列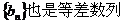 ,类比上述性质,相应地若数列
,类比上述性质,相应地若数列 >0,
>0, ,则有
,则有
正确答案:
错误原因:类比意识不强
5.已知数列 是非零等差数列,又a1,a3,a9组成一个等比数列的前三项,则
是非零等差数列,又a1,a3,a9组成一个等比数列的前三项,则 的值是
。
的值是
。
答案:1或
错解: 错因:忘考虑公差为零的情况。
错因:忘考虑公差为零的情况。
4.关于数列有下列四个判断:
(1)若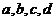 成等比数列,则
成等比数列,则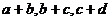 也成等比数列;
也成等比数列;
(2)若数列{ }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{ }为常数列;
}为常数列;
(3)数列{ }的前n项和为
}的前n项和为 ,且
,且 ,则{
,则{ }为等差或等比数列;
}为等差或等比数列;
(4)数列{ }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{ }中不会有
}中不会有 ,其中正确判断的序号是______(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______(注:把你认为正确判断的序号都填上)
正解:(2)(4).
误解:(1)(3)。对于(1)a、b、c、d成等比数列。
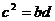

 也成等比数列,这时误解。因为特列:
也成等比数列,这时误解。因为特列: 时,
时,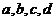 成等比数列,但
成等比数列,但 ,
, ,
, ,即
,即 不成等比。
不成等比。
对于(3)可证当 时,为等差数列,
时,为等差数列, 时为等比数列。
时为等比数列。
 时既不是等差也不是等比数列,故(3)是错的。
时既不是等差也不是等比数列,故(3)是错的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com