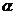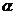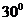7.　　　 (如中)点AB到平面距离分别为12，20，若斜线AB与成的角，则AB的长等于_____.

错解：16. 错误原因是只考虑AB在平面同侧的情形，忽略AB在平面两测的情况。正确答案是：16或64。

6.　　　 (如中)平面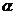外有两点A,B，它们与平面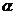的距离分别为a,b，线段AB上有一点P，且AP:PB=m:n，则点P到平面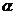的距离为_________________.

错解为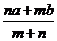：。错误原因是只考虑AB在平面同侧的情形，忽略AB在平面两测的情况。正确答案是：。

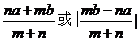5.　　　 (如中)判断题：若两个平面互相垂直，过其中一个平面内一点作它们的交线的垂线，则此直线垂直于另一个平面。

正确。错误原因是未能认真审题或空间想象力不够，忽略过该点向平面外作垂线的情况。正确答案是本题不对。

4.　　　 (如中)过球面上两已知点可以作的大圆个数是_________个。

错解：1个。错误原因是没有注意球面上两已知点与球心共线的特殊情况，可作无数个。

正确答案是不能确定。

3.　　　 (如中)已知正三棱柱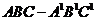底面边长是10，高是12，过底面一边AB，作与底面ABC成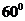角的截面面积是___________________。

错解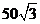：。学生用面积射影公式求解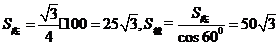：。错误原因是没有弄清截面的形状不是三角形而是等腰梯形。正确答案是：。

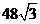2.　　　 (如中)一个广告气球某一时刻被一束平行光线投射到水平地面上的影子是一个椭圆，椭圆的离心率为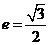，则该时刻这平行光线对于水平平面的入射角为________。

错解：答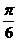。错误原因是概念不清，入射角应是光线与法线的夹角，正确答案为：。

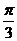1.　　　 (如中)有一棱长为a的正方体骨架，其内放置一气球，使其充气且尽可能地大(仍保持为球的形状)，则气球表面积的最大值为__________.

错解：学生认为球最大时为正方体的内切球，所以球的直径为a，球的表面积为。这里学生未能弄清正方体骨架是一个空架子，球最大时与正方体的各棱相切，直径应为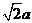，所以正确答案为：。

24．(案中)给出下列四个命题：

(1)　　　 各侧面都是正方形的棱柱一定是正棱柱

(2)　　　 若一个简单多面体的各顶点都有三条棱，则其顶点数V，面数F满足的关系式为2F-V=4

(3)　　　 若直线L⊥平面α，L∥平面β，则α⊥β

(4)　　　 命题“异面直线a,b不垂直，则过a的任一平面和b都不垂直”的否定，其中，正确的命题是　　 (　　 )

　 A、(2)(3)　　 B、(1)(4)　　 C、(1)(2)(3)　　 D、(2)(3)(4)

正确答案：(A)

错误原因：易认为命题(1)正确

二填空题：

23．(案中)底面是正三角形，且每个侧面是等腰三角形的三棱锥是

A、一定是正三棱锥　 B、一定是正四面体　 C、不是斜三棱锥　 D、可能是斜三棱锥

正确答案：(D)

错误原因：此是正三棱锥的性质，但很多学生凭感觉认为如果侧面是等腰三角形，则侧棱长相等，所以一定是正三棱锥，事实上，只须考察一个正三角形绕其一边抬起后所构成的三棱锥就知道应选D

22．(薛中)空间四边形中，互相垂直的边最多有(　　 )

　　 A、1对　　　 B、2对　　　 C、3对　　　 D、4对

　　 答案：C

　　 错解：D

　　 错因：误将空间四边形理解成四面体，对“空间四边形”理解不深刻。