
1、该三棱柱的侧面展开图的对角线长;
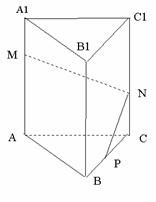
7.(江安中学)如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M点的最短路线长为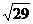 ,设这条最短路线与C1C的交点为N。求
,设这条最短路线与C1C的交点为N。求
6.(江安中学)如图在三棱柱ABC-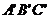 中,已知底面ABC是底角等于
中,已知底面ABC是底角等于 ,底边AC=
,底边AC= 的等腰三角形,且
的等腰三角形,且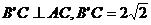 ,面
,面 与面ABC成
与面ABC成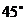 ,
, 与
与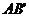 交于点E。
交于点E。
1)
 求证:
求证: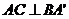 ;
;
2)
求异面直线AC与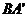 的距离;
的距离;
3)
求三棱锥 的体积。
的体积。
正解:①证:取AC中点D,连ED,
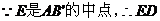 //
//

又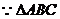 是底角等于
是底角等于 的等腰
的等腰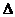 ,
,
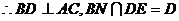

②解:由①知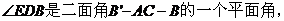
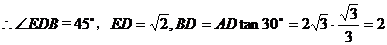
在
 是异面直线AC与
是异面直线AC与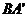 的距离,为
的距离,为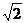
③连

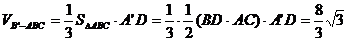
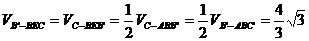
误解:求体积,不考虑用等积法,有时,硬算导致最后错解。
5.(蒲中)斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成450角,求这个三棱柱的侧面积。
解:过点B作BM⊥AA1于M,连结CM,在△ABM和△ACM中,∵AB=AC,∠MAB=∠MAC=450,MA为公用边,∴△ABM≌△ACM,∴∠AMC=∠AMB=900,∴AA1⊥面BHC,即平面BMC为直截面,又BM=CM=ABsin450= a,∴BMC周长为2x
a,∴BMC周长为2x a+a=(1+
a+a=(1+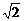 )a,且棱长为b,∴S侧=(1+
)a,且棱长为b,∴S侧=(1+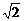 )ab
)ab
点评:本题易错点一是不给出任何证明,直接计算得结果;二是作直截面的方法不当,即“过BC作平面与AA1垂直于M”;三是由条件“∠A1AB=∠A1AC ∠AA1在底面ABC上的射影是∠BAC的平分线”不给出论证。
∠AA1在底面ABC上的射影是∠BAC的平分线”不给出论证。
4.(一中)点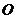 是边长为4的正方形
是边长为4的正方形 的中心,点
的中心,点 ,
, 分别是
分别是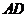 ,
,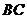 的中点.沿对角线
的中点.沿对角线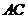 把正方形
把正方形 折成直二面角D-AC-B.
折成直二面角D-AC-B.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求二面角 的大小.
的大小.
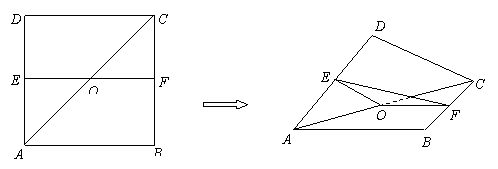 解法一:(Ⅰ)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则
解法一:(Ⅰ)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则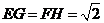 ,
, .
.
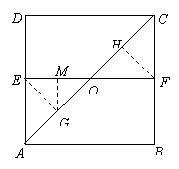
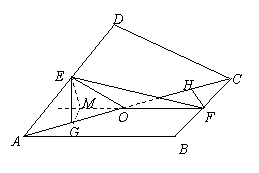
因为二面角D-AC-B为直二面角,
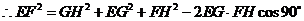
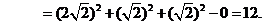
又在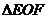 中,
中,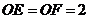 ,
,
 .
.
 .
.
(Ⅱ)过点G作GM垂直于FO的延长线于点M,连EM.
 ∵二面角D-AC-B为直二面角,∴平面DAC⊥平面BAC,交线为AC,又∵EG⊥AC,∴EG⊥平面BAC.∵GM⊥OF,由三垂线定理,得EM⊥OF.
∵二面角D-AC-B为直二面角,∴平面DAC⊥平面BAC,交线为AC,又∵EG⊥AC,∴EG⊥平面BAC.∵GM⊥OF,由三垂线定理,得EM⊥OF.
∴ 就是二面角
就是二面角 的平面角.
的平面角.
在Rt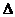 EGM中,
EGM中, ,
,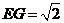 ,
, ,
,
∴ .
.
∴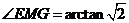 .
.
所以,二面角 的大小为
的大小为 .
.
解法二:(Ⅰ)建立如图所示的直角坐标系O-xyz,
则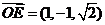 ,
, .
.
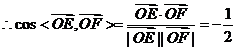 .
.
 .
.
(Ⅱ)设平面OEF的法向量为 .
.
由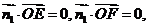 得
得
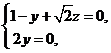 解得
解得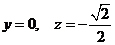 .
.
所以,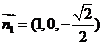 .
.
又因为平面AOF的法向量为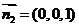 ,
,
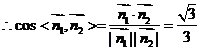 .∴
.∴ .
.
 所以,二面角
所以,二面角 的大小为
的大小为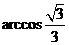 .
.
3. (石庄中学)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求: (1)
(石庄中学)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求: (1)
 ;
;
(2) 直线AD与平面ANM所成的角的大小;
(3) 平面ANM与平面ABCD所成角(锐角)的大小.
解:(1) 以A为原点,AB、AD、AA1所在直线为x轴,y轴,z轴.
则D(0,8,0),A1 (0,0,4),M(5,2,4)
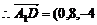 )
)
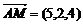
∵ ∴
∴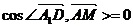
(2) 由(1)知A1D⊥AM,又由已知A1D⊥AN, 平面AMN,垂足为N.
平面AMN,垂足为N.
因此AD与平面所成的角即是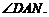
易知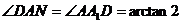
(3) ∵ 平面ABCD,A1N
平面ABCD,A1N 平面AMN,
平面AMN,
∴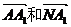 分别成为平面ABCD和平面AMN的法向量。
分别成为平面ABCD和平面AMN的法向量。
设平面AMN与平面ABCD所成的角(锐角)为 ,则
,则
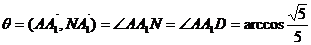
2. (如中)一个棱长为6cm的密封正方体盒子中放一个半径为1cm的小球,无论怎样摇动盒子,求小球在盒子不能到达的空间的体积。
错解:认为是正方体的内切球。用正方体的体积减去内切球的体积。
错误原因是空间想像力不够。
正解:在正方体的8个顶点处的单位立方体空间内,小球不能到达的空间为: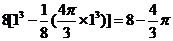 ,除此之外,在以正方体的棱为一条棱的12个
,除此之外,在以正方体的棱为一条棱的12个 的正四棱柱空间内,小球不能到达的空间共为
的正四棱柱空间内,小球不能到达的空间共为 。其他空间小球均能到达。故小球不能到达的空间体积为:
。其他空间小球均能到达。故小球不能到达的空间体积为:
 。
。
1.
(如中)由平面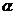 外一点P引平面的三条相等的斜线段,斜足分别为ABC,O为⊿ABC的外心,求证:
外一点P引平面的三条相等的斜线段,斜足分别为ABC,O为⊿ABC的外心,求证: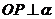 。
。
错解:因为O为⊿ABC的外心,所以OA=OB=OC,又因为PA=PB=PC,PO公用,所以⊿POA,⊿POB,⊿POC都全等,所以 POA=
POA= POB=
POB= POC=RT
POC=RT ,所以
,所以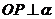 。
。
错解分析:上述解法中 POA=
POA= POB=
POB= POC=RT
POC=RT ,是对的,但它们为什么是直角呢?这里缺少必要的证明。
,是对的,但它们为什么是直角呢?这里缺少必要的证明。
正解:取BC的中点D,连PD,OD,
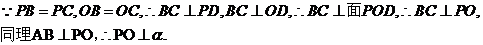
29.(案中)点P在直径为2的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和为最大值是
正确答案:
错误原因:找不到解题思路
28.(案中)在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是AB和AD的中点,则点A1到平面为EF的距离为
正确答案:
错误原因:不少学生能想到用等积法解,但运算存在严重问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com