
14.时人认为刘半农为人治学都浅,你同意不同意这种看法?请结合文本,联系现实,谈谈你的看法。(6分 )
)
答:
13.结合文中的主要事例,归纳概括刘半农的形象特点。(4分)
答:
12.下列对作品的分析和概括,不正确的两项是(5分)( )
A.陈独秀和胡适作为 “新文化运动”的领军人物,他们在对敌斗争中都比较讲究韬略,但两人所采用的韬略却各不相同。
B.刘半农诙谐幽默,不拘小节。因而写出了《教我如何不想她》这样风行一时的流行歌歌词。
C.文章标题中“教我如何不想她”既是全文的线索,又揭示了文章的主旨,也表达了后人及友人对刘半农先生的怀念之情。
D.时人评论刘半农时,送其一“浅”字。 一是因为他“胸无城府,浅如清溪”; 二是因为他所学颇杂,对所学内容缺乏深入的研究。
E.在众友吊唁的挽联中,刘半农生前挚交赵元任写得最为贴切,挽联的字里行间饱含了他对刘半农的深切怀念之情。
2. 某厂生产甲产品每千克需用原料A、原料B分别为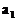 千克、b1千克,生产乙产品每千克需用原料A、原料B分别为a2千克、b2千克,甲、乙产品每千克可获利润分别为d1元、d2元。月初一次性购进本月所需原料A、B分别为c1千克、c2千克,则本月生产甲产品和乙产品分别为多少千克才能使月利润总额达到最大?在这个问题中,设全月生产甲、乙两种产品分别为x千克、y千克,月利润总额为z元,那么,用于求使总利润
千克、b1千克,生产乙产品每千克需用原料A、原料B分别为a2千克、b2千克,甲、乙产品每千克可获利润分别为d1元、d2元。月初一次性购进本月所需原料A、B分别为c1千克、c2千克,则本月生产甲产品和乙产品分别为多少千克才能使月利润总额达到最大?在这个问题中,设全月生产甲、乙两种产品分别为x千克、y千克,月利润总额为z元,那么,用于求使总利润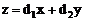 最大的数学模型中,约束条件为( )
最大的数学模型中,约束条件为( )
A. 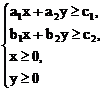 B.
B.
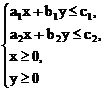
C. 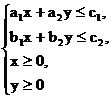 D.
D.
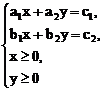
例5. 在平面直角坐标系中,不等式组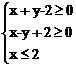 ,表示的平面区域的面积是( )
,表示的平面区域的面积是( )
A. 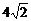 B.
4 C.
2
B.
4 C.
2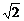 D.
2
D.
2
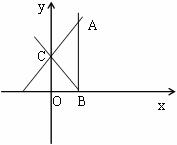
由题知可画出可行域为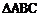 (如上图),
(如上图),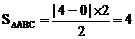 ,故选择B。
,故选择B。
点评:本题考查简单的线性规划的可行域(三角形)的面积,同时切记做线性规划的题目时,最关键的是不等号的处理,应考虑要求的区域是在直线的上方还是下方。
练一练
1. 已知点P(x,y)的坐标满足条件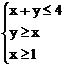 点O为坐标原点,那么|PO|的最小值等于_______,最大值等于_________。
点O为坐标原点,那么|PO|的最小值等于_______,最大值等于_________。
例4. 双曲线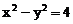 的两条渐近线与直线x=3围成一个三角形区域,表示该区域的不等式组是( )
的两条渐近线与直线x=3围成一个三角形区域,表示该区域的不等式组是( )
A. 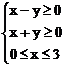 B.
B.
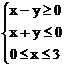 C.
C.
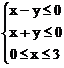 D.
D.
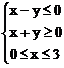
双曲线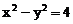 的两条渐近线方程为
的两条渐近线方程为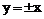 ,两者与直线
,两者与直线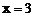 围成一个三角形区域时有
围成一个三角形区域时有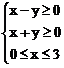 ,故
,故
选A。
点评:本题考查了双曲线的渐近线方程以及线性规划问题。
例3. 已知变量x,y满足约束条件 。若目标函数
。若目标函数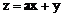 (其中
(其中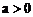 )仅在点(3,1)处取得最大值,则a的取值范围为_________。
)仅在点(3,1)处取得最大值,则a的取值范围为_________。
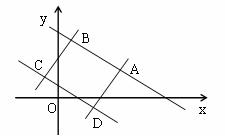
解:由已知变量满足约束条件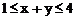 ,
,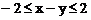 。在坐标系中画出可行域,如图为四边形ABCD,其中A(3,1),
。在坐标系中画出可行域,如图为四边形ABCD,其中A(3,1),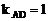 ,
,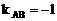 。目标函数
。目标函数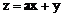 (其中
(其中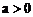 )可转化为
)可转化为 表示斜率为
表示斜率为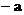 的直线系中的截距的大小,若仅在点A处取得最大值,则斜率应小于
的直线系中的截距的大小,若仅在点A处取得最大值,则斜率应小于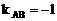 ,即
,即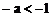 ,所以a的取值范围为(1,
,所以a的取值范围为(1, )
)
例1. 在约束条件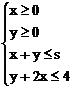 下,当
下,当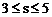 时,目标函数
时,目标函数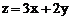 的最大值的变化范围是( )
的最大值的变化范围是( )
A. [6,15] B. [7,15] C. [6,8] D. [7,8]
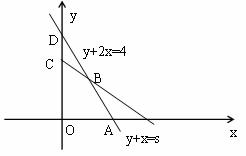
解:由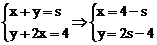 则由题意知A(0,2),B(
则由题意知A(0,2),B(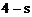 ,
,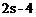 ),C(0,s),D(0,4)。
),C(0,s),D(0,4)。
(1)当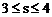 时可行域是四边形OABC,此时,
时可行域是四边形OABC,此时,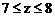 ;
;
(2)当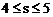 时可行域是
时可行域是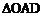 ,此时,
,此时,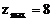 。
。
由以上可知,正确答案为D。
点评:本题主要考查线性规划的基础知识,借助图形解题。
例2. 已知平面区域D由以A(1,3)、B(5,2)、C(3,1)为顶点的三角形内部和外界组成。若在区域D内有无穷多个点(x,y)可使目标函数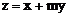 取得最小值,则m=( )
取得最小值,则m=( )
A. 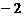 B.
B.
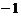 C.
1 D.
4
C.
1 D.
4
解:由A(1,3)、B(5,2)、C(3,1)的坐标位置知,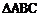 所在的区域在第一象限,故
所在的区域在第一象限,故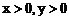 。当
。当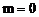 时,z=x,只有一个点为最小值,不合题意。当
时,z=x,只有一个点为最小值,不合题意。当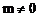 时,由z=x+my得
时,由z=x+my得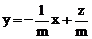 ,它表示的直线的斜率为
,它表示的直线的斜率为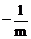 。
。
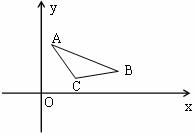
(1)若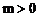 ,则要使
,则要使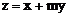 取得最小值,必须使
取得最小值,必须使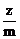 最小,此时需
最小,此时需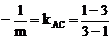 ,即m=1;
,即m=1;
(2)若m<0,则要使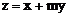 取得最小值,必须使
取得最小值,必须使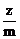 最大,此时需
最大,此时需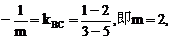 与m<0矛盾。
与m<0矛盾。
综上可知,m=1。
点评:本题主要考查同学们运用线性规划的基础知识与分类讨论的数学思想综合解决问题的能力。
3、平面NMP和平面ABC所成二面角(锐角)的大小(用反三角函数表示)
 正解:①正三棱柱ABC-A1B1C1的侧面展开图是一个长为9,宽为4的矩形,其对角线长为
正解:①正三棱柱ABC-A1B1C1的侧面展开图是一个长为9,宽为4的矩形,其对角线长为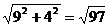
②如图1,将侧面BC1旋转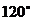 使其与侧面AC1在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱柱侧面经过CC1到点M的最短路线。
使其与侧面AC1在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱柱侧面经过CC1到点M的最短路线。
设PC=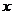 ,则P1C=
,则P1C=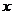 ,
,
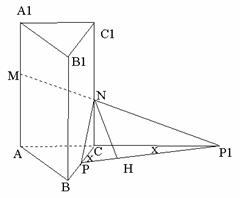 在
在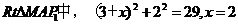
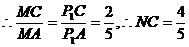
③连接PP1(如图2),则PP1就是NMP与平面ABC的交线,作NH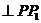 于H,又CC1
于H,又CC1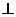 平面ABC,连结CH,由三垂线定理得,
平面ABC,连结CH,由三垂线定理得,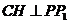 。
。

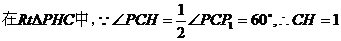
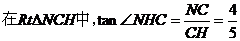
误解:①不会找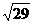 的线段在哪里。
的线段在哪里。
②不知道利用侧面BCC1 B1展开图求解。
③不会找二面角的平面角。
2、PC和NC的长;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com