
6.下列说法正确的是:( )
A.2009年12月中旬在哥本哈根召开的国际气候会议受到全球政要的广泛关注,减缓工业生产大量排放二氧化硫以抑制全球气候变暖成为该会议的主题
B.用乙炔与氯化氢合成氯乙烯中,其原子利用率为100﹪符合化学原子经济性要求,
C.工业上中用甲醇质子交换膜燃料电池将甲醇蒸气转化为氢气;△H=-192.9kJ·mol-1,其热化学方程式可表示为:
CH3OH(l)+1/2O2(g)=CO2(g)+2H2(g);△H=-192.9kJ·mol-1
D.合成氨气工业中根据勒下特列原理,选取高压和适当的催化剂以提高氨的转换率
22.解:(1)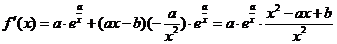
令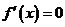 得
得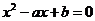
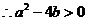 又
又 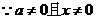
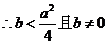 ………………4分
………………4分
(2)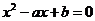 在
在 有两个不相等的实根.
有两个不相等的实根.
即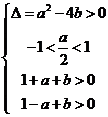 得
得 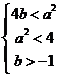
所以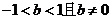 ………………8分
………………8分
(3)由①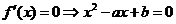
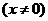
①当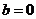 ,
,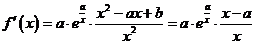 在
在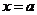 左右两边异号
左右两边异号
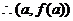 是
是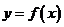 的唯一的一个驻点
的唯一的一个驻点
由题意知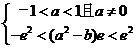 即
即 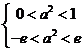 即
即 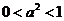
存在这样的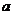 满足题意
满足题意
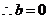 符合题意
………………10分
符合题意
………………10分
②当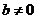 时,
时,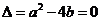 即
即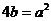
这时函数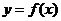 唯一的一个驻点为
唯一的一个驻点为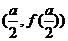
由题意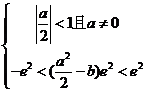
即 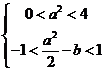 即
即 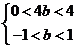
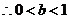 ………………………………14分
………………………………14分
综合①②知:满足题意 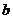 的范围为
的范围为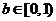 . ……………………………15分
. ……………………………15分
21.解:(1) 设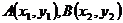
由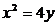 ,得
,得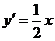
则过点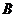 的切线方程为:
的切线方程为:
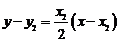 ,即
,即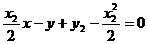
由已知: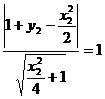 ,又
,又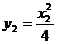 ,
,
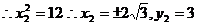 ,
,
即点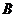 坐标为
坐标为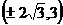 ,
,
 直线
直线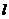 的方程为:
的方程为: .
(7分)
.
(7分)
(Ⅱ)由已知,直线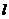 的斜率存在,则设直线
的斜率存在,则设直线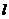 的方程为:
的方程为: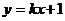 ,
,
联立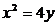 ,得
,得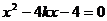
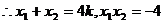
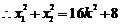 (9分)
(9分)
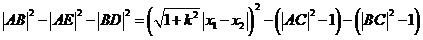 (11分)
(11分)
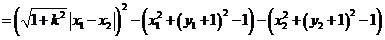

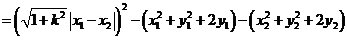
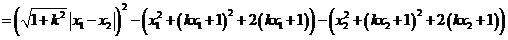 (13分)
(13分)
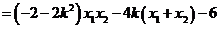 =
=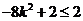
所以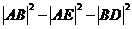 的取值范围是
的取值范围是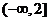 。
(15分)
。
(15分)
20、解: (1)当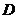 为
为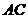 中点时,有
中点时,有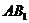 ∥平面
∥平面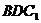 .…1分
.…1分
 证明:连结
证明:连结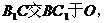 连结
连结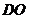 ,
,
∵四边形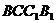 是矩形 ∴
是矩形 ∴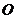 为
为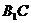 中点
中点
∵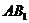 ∥平面
∥平面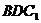 ,
,
且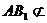 平面
平面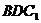 ,
,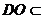 平面
平面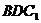
∴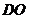 ∥
∥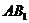 ,------------------5分
,------------------5分
∴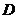 为
为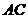 的中点.------------------6分
的中点.------------------6分
(2)建立空间直角坐标系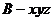 如图所示,
如图所示,
则 ,
,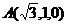 ,
,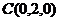 ,
,
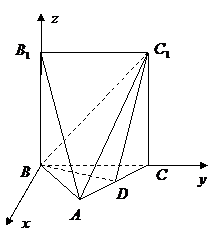
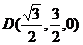 ,
,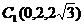 ------------8分
------------8分
所以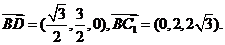
设 为平面
为平面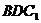 的法向量,
的法向量,
则有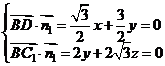 ,
,
即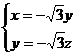
令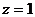 ,可得平面
,可得平面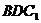 的一个
的一个
法向量为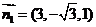 , ----------------11分
, ----------------11分
而平面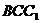 的法向量为
的法向量为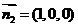 , ---------------------------12分
, ---------------------------12分
所以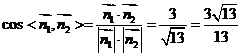 ,
,
所以二面角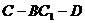 的余弦值为
的余弦值为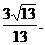 ----------------------------14分
----------------------------14分
19.(1)由条件: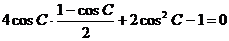
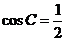 ………………(3分)
………………(3分)
故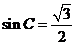 ,则
,则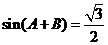 ,
,
由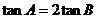 ,得
,得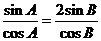 , 所以
, 所以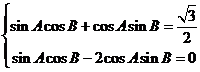 ,
,
得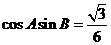 ,
, ,
,
所以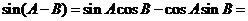
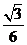 (7分)
(7分)
(2)由余弦定理: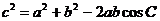

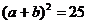

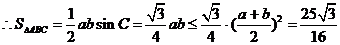
当且仅当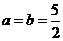 取得最大值.
(14分)
取得最大值.
(14分)
18.解:(1)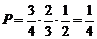 ;…………………………………………4分
;…………………………………………4分
(2)提示: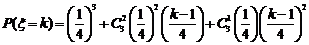 ,
,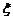 的分布列为:
的分布列为:
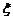 |
1 |
2 |
3 |
4 |
|
P |
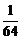 |
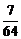 |
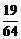 |
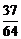 |
………………………………(建议对1个给2分)…………………………………………12分
故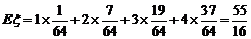 .………………………………………………14分
.………………………………………………14分
16.2016 17.②③
11.90 12.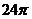 13.
13. 14.
14.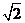 15.
15.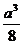
1.D 2.B 3.A 4.D 5.C 6.A 7.D 8.C 9.A 10.D
22.(本小题满分15分)
设函数 的导函数为
的导函数为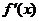 ,若
,若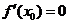 ,则称点
,则称点 是函数
是函数 的一个驻点。已知函数
的一个驻点。已知函数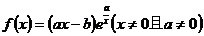
(1)若函数 总存在有两个驻点
总存在有两个驻点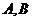 ,求
,求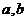 所满足的关系;
所满足的关系;
(2)若函数 有两个驻点
有两个驻点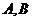 ,且存在
,且存在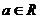 ,求
,求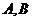 两个驻点在不等式
两个驻点在不等式 表示的区域内时实数
表示的区域内时实数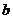 的范围;
的范围;
(3)若函数 恰有一个驻点
恰有一个驻点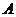 ,且存在
,且存在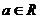 ,使驻点
,使驻点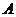 在不等式
在不等式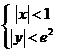 表示的区域内,证明:
表示的区域内,证明: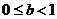 .
.
浙江省杭州高级中学高三理科数学月考试卷(2010.3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com