
4.由直线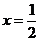 ,x=2,曲线
,x=2,曲线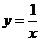 及x轴所围图形的面积为( )
及x轴所围图形的面积为( )
 A.
A.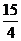 B.
B.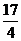 C.
C.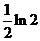 D.
D.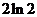
3. 设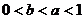 ,则下列不等式成立的是
( )
,则下列不等式成立的是
( )
A. 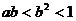 B.
B.
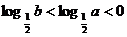
C.  D.
D.
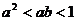
2. 已知 为第二象限的角,且
为第二象限的角,且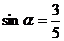 ,则
,则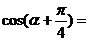 ( )
( )
A.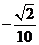 B.
B.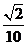 C.
C.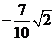 D.
D.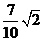
1.设复数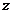 满足
满足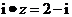 ,则
,则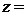 ( )
( )
A.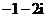 B.
B.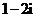 C.
C.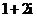 D.
D.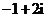
23、(18分) 对于定义在D上的函数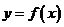 ,若存在
,若存在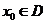 ,对任意的
,对任意的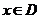 ,都有
,都有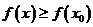 ,则称函数
,则称函数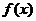 在区间
在区间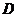 上有下界,把
上有下界,把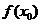 称为函数
称为函数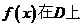 的“下界”。
的“下界”。
(1)分别判断下列函数是否有“下界”?如果有,写出“下界”否则请说明理由;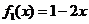
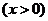 ,
,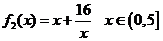
(2)请你类比函数有“下界”的定义,写出函数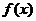 在区间
在区间 上有“上界”的定义;并判断函数
上有“上界”的定义;并判断函数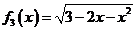 是否有“上界”?说明理由;
是否有“上界”?说明理由;
(3)若函数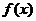 在区间
在区间 上既有“上界”又有“下界”,则称函数
上既有“上界”又有“下界”,则称函数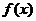 是区间
是区间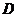 上的“有界函数”,把“上界”减去
“下界”的差称为函数
上的“有界函数”,把“上界”减去
“下界”的差称为函数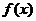 在
在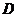 上的“幅度
上的“幅度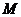 ”。
”。
对于实数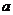 ,试探究函数
,试探究函数 是否是
是否是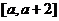 上的“有界函数”?如果是,求出“幅度
上的“有界函数”?如果是,求出“幅度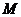 ”的值。
”的值。
上海市部分重点中学高三第二次联考
22、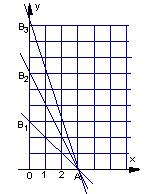 (18分)在平面直角坐标系上,设不等式组
(18分)在平面直角坐标系上,设不等式组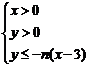 (
(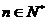 )
)
所表示的平面区域为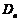 ,记
,记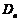 内的整点(即横坐标和纵坐标均
内的整点(即横坐标和纵坐标均
为整数的点)的个数为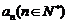 .
.
(1)求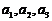 并猜想
并猜想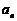 的表达式(不必证明)
的表达式(不必证明)
(2)设数列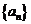 的前项和为
的前项和为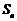 ,数列
,数列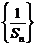 的前项和
的前项和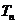 ,
,
求使不等式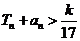 对一切nÎN*都成立的最大正整数k的值;
对一切nÎN*都成立的最大正整数k的值;
(3)设nÎN*,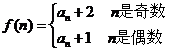 问是否存在mÎN*,使
问是否存在mÎN*,使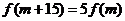 成立?若存在,求出m的值;若不存在,请说明理由.
成立?若存在,求出m的值;若不存在,请说明理由.
21、(16分)在直角坐标系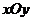 中,动点
中,动点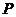 到两点
到两点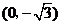 ,
,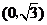 的距离之和
的距离之和
等于4,设动点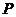 的轨迹为
的轨迹为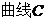 ,直线
,直线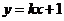 与
与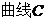 交于
交于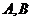 两点.
两点.
(1)写出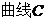 的方程;
的方程;
(2)当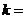 1时,求三角形
1时,求三角形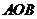 的面积
的面积
(3)若 ,求k的值
,求k的值
20、 (14分)如图直三棱柱
(14分)如图直三棱柱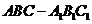 的侧棱长为2,底面
的侧棱长为2,底面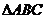 是等腰直角三角形,
是等腰直角三角形,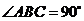 ,
,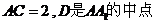
(1)求异面直线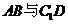 所成的角的大小;
所成的角的大小;
(2 )求直线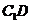 与平面
与平面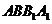 所成的角;
所成的角;
19、(12分)已知复数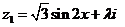 ,
,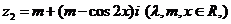 且
且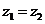 .
.
(1)若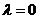 且
且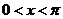
 ,求
,求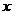 的值;
的值;
(2)设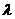 =
=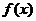 ,求
,求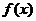 的最小正周期和单调增区间.
的最小正周期和单调增区间.
解:
18、已知集合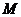 是满足下列性质的函数
是满足下列性质的函数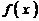 的全体:
的全体:
当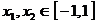 时,都有
时,都有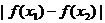
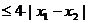 ,
,
在以下函数①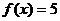 ;②
;②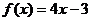 ;③
;③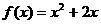 ;④
;④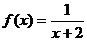 中
中
可以是集合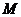 中的元素的序号为( )
中的元素的序号为( )
(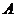 )①②③④; (
)①②③④; (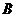 )①②④;
(
)①②④;
(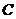 )②③; (
)②③; ( )①②③。
)①②③。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com