

20.(本小题满分14分)
已知数列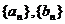 ,其中
,其中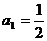 ,数列
,数列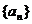 的前n项和
的前n项和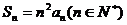 ,数列
,数列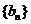 满足b1=2,bn+1=2bn.
满足b1=2,bn+1=2bn.
(1)求数列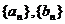 的通项公式;
的通项公式;
(2)是否存在自然数m,使得对于任意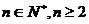 ,有
,有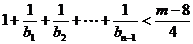 恒成立?若存在,求出m的最小值;
恒成立?若存在,求出m的最小值;
(3)若数列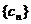 满足
满足
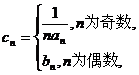 求数列
求数列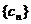 的前n项和Tn.
的前n项和Tn.
19.(本小题满分13分)
已知椭圆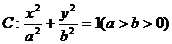 的离心率为
的离心率为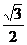 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线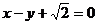 相切.
相切.
(1)求椭圆C的方程;
(2)设P(4,0),M,N是椭圆C上关于x轴对称的任意两个不同的点,连结PN交椭圆C于另一点E,求直线PN的斜率的取值范围;
(3)在(2)的条件下,证明直线ME与x轴相交于定点.
18.(本小题满分13分)
已知函数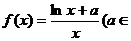 R).
R).
(1)若曲线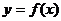 在点
在点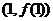 处的切线与直线
处的切线与直线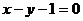 平行,求a的值;
平行,求a的值;
(2)求函数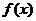 的单调区间和极值;
的单调区间和极值;
(3)当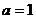 ,且
,且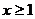 时,证明:
时,证明: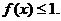
17.(本小题满分14分)
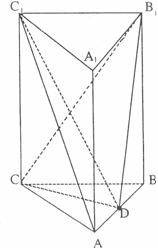
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC
是边长为2的等边三角形,D为AB边中点,且CC1=2AB.
(1)求证:平面C1CD⊥平面ABC;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥D-CBB1的体积.
16.(本小题满分13分)
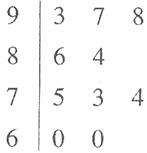
在一次数学统考后,某班随机抽取10名同学的成绩进行
样本分析,获得成绩数据的茎叶图如下.
(1)计算样本的平均成绩及方差;
(2)在这10个样本中,现从不低于84分的成绩中随机抽取
2个,求93分的成绩被抽中的概率.
15.(本小题满分13分)
设函数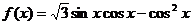
(1)求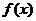 的最小正周期;
的最小正周期;
(2)当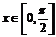 时,求函数
时,求函数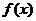 的最大值和最小值.
的最大值和最小值.
14.点P是椭圆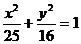 上一点,F1,F2是椭圆的两个焦点,且△PF1F2的内切圆半径为1,当P在第一象限时,P点的纵坐标为
.
上一点,F1,F2是椭圆的两个焦点,且△PF1F2的内切圆半径为1,当P在第一象限时,P点的纵坐标为
.
13.向量a,b满足: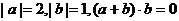 ,则a与b的夹角是
.
,则a与b的夹角是
.
12.海上有A,B,C三个小岛,测得A,B两岛相距10n mile,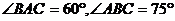 ,则B,C间的距离是
n mile.
,则B,C间的距离是
n mile.
11.设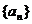 是等比数列,若
是等比数列,若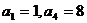 ,则q=
,数列
,则q=
,数列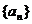 的前6项的和S6= .
的前6项的和S6= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com