
4. 若等差数列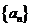 的前5项和
的前5项和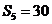 ,且
,且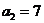 ,则
,则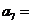 ( )
( )
A.0 B.1 C.2 D.3
3. 在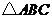 中,若
中,若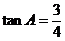 ,
,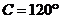 ,
,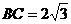 ,则
,则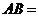 ( )
( )
A.3 B.4 C.5 D.6
2. 已知复数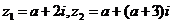 ,且
,且 ,则实数a的值为( )
,则实数a的值为( )
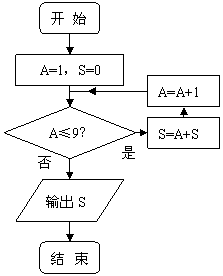 A. 0 B. -5 C.
0或-5 D. 0或5
A. 0 B. -5 C.
0或-5 D. 0或5
1. 已知集合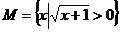 ,集合
,集合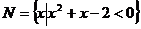 ,则
,则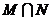 =( )
=( )
A.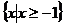 B.
B.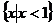 C.
C. 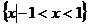 D.
D. 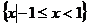
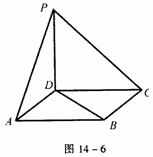
例20 如图14-6,点P在正方形ABCD所在的平面外,PD⊥ABCD,PD=AD,则PA与BD所成角的度数为 。
解 根据题意可将上图补形成一正方体,在正方体中易求得为60°。
8.特殊模型法
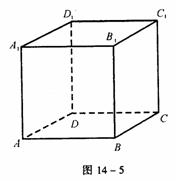
例19 已知m,n是直线,α、β、γ是平面,给出下列命题:
①若α⊥γ,β⊥γ,则α∥β;
②若n⊥α,n⊥β,则α∥β;
③若α内不共线的三点到β的距离都相等,则α∥β;
④若n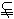 α,m
α,m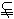 α,且n∥β,m∥β,则α∥β;
α,且n∥β,m∥β,则α∥β;
⑤若m,n为异面直线,n∈α,n∥β,m∈β,m∥α,则α∥β;
则其中正确的命题是 。(把你认为正确的命题序号都填上)
解 依题意可构造正方体AC1,如图14-5,在正方体中逐一判断各命题易得正确命题的是②⑤。
7.特殊方程法
例18 直线l过抛物线y2=a(x+1)(a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a= 。
解 ∵抛物线y2=a(x+1)与抛物线y2=ax具有相同的垂直于对称轴的焦点弦长,故可用标准方程y2=ax替换一般方程y2=a(x+1)求解,而a值不变。由通径长公式得a=4。
6.特殊点法
例17 椭圆 +
+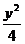 =1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是 。
=1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是 。
解 设P(x,y),则当∠F1PF2=90°时,点P的轨迹方程为x2+y2=5,由此可得点P的横坐标x=±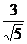 ,又当点P在x轴上时,∠F1PF2=0;点P在y轴上时,∠F1PF2为钝角,由此可得点P横坐标的取值范围是-
,又当点P在x轴上时,∠F1PF2=0;点P在y轴上时,∠F1PF2为钝角,由此可得点P横坐标的取值范围是-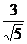 <x<
<x<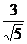 。
。
5.图形特殊位置法
例16 已知SA,SB,SC两两所成角均为60°,则平面SAB与平面SAC所成的二面角为 。
解 取SA=SB=SC,将问题置于正四面体中研究,不难得平面SAB与平面SAC所成的二面角为arccos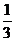 。
。
3.特殊角法
例14 cos2α+cos2(α+120°)+cos2(α+240°)的值为 。
解 本题的隐含条件是式子的值为定值,即与α无关,故可令α=0°,计算得上式值为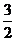 。
。
例15 已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则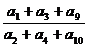 的值是 。
的值是 。
解 考虑到a1,a3,a9的下标成等比数列,故可令an=n,又易知它满足题设条件,于是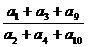 =
=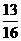 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com