
20.已知抛物线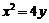 上的点
上的点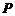 (非原点)处的切线与
(非原点)处的切线与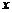 轴,
轴,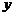 轴分别交于
轴分别交于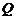 ,
,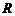 两点,
两点,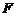 为焦点.
为焦点.
 ⑴若
⑴若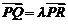 ,求
,求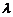 的取值范围;
的取值范围;
⑵若抛物线上的点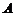 满足条件
满足条件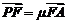 ,求
,求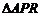 面积的最小值,并写出此时的切线方程.
面积的最小值,并写出此时的切线方程.
19.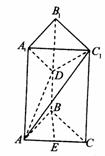 如图所示,在直三棱柱
如图所示,在直三棱柱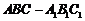 中,已知
中,已知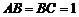 ,
,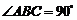 ,
,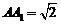 ,
,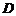 ,
,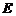 分别为
分别为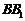 、
、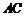 的中点.
的中点.
⑴证明: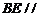 平面
平面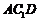 ;
;
⑵求二面角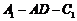 的大小.
的大小.
18.设函数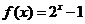 的反函数为
的反函数为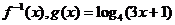
⑴若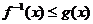 ,求
,求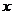 的取值范围D;
的取值范围D;
⑵设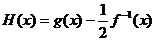 ,当
,当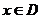 时,求函数
时,求函数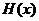 的值域.
的值域.
17.设数列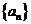 满足:
满足: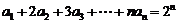
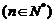 .
.
⑴求数列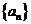 的通项公式;
的通项公式;
⑵设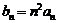 ,求数列
,求数列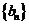 的前
的前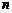 项和
项和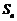 .
.
16.在锐角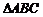 中,
中,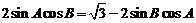 ,边
,边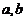 是方程
是方程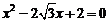 的两个实根.
的两个实根.
求:⑴求角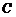 的值;⑵三角形面积
的值;⑵三角形面积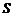 及边
及边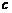 的长.
的长.
15.
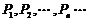 顺次为函数
顺次为函数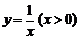 图象上的点(如图)
图象上的点(如图)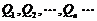 顺次为
顺次为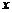 轴上的点,且
轴上的点,且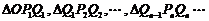 均为等腰直角三角形(其中
均为等腰直角三角形(其中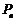 为直角顶点),设
为直角顶点),设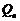 的坐标为(
的坐标为(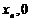 )
)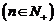 ,则数列
,则数列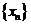 的通项公式为____________.
的通项公式为____________.
14.对于函数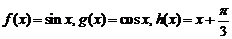 ,有如下三个命题:
,有如下三个命题:
①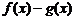 的最大值为
的最大值为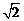 ;
;
②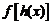 在区间
在区间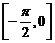 上是增函数;
上是增函数;
③将 的图象向右平移
的图象向右平移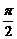 个单位可得
个单位可得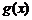 的图象,其中真命题的序号是__________.
的图象,其中真命题的序号是__________.
13.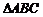 中,
中,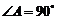 ,
,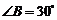 ,椭圆以
,椭圆以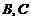 为焦点,且经过
为焦点,且经过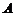 点,则椭圆离心率
点,则椭圆离心率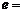 ___________.
___________.
12.已知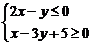 ,则
,则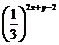 的最小值是___________.
的最小值是___________.
11.已知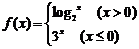 ,则
,则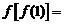 ____________.
____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com