

18.(本小题满分16分)
已知在△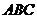 中,点
中,点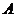 、
、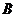 的坐标分别为
的坐标分别为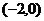 和
和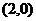 ,点
,点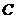 在
在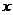 轴上方.
轴上方.
(Ⅰ)若点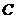 的坐标为
的坐标为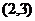 ,求以
,求以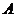 、
、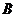 为焦点且经过点
为焦点且经过点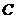 的椭圆的方程;
的椭圆的方程;
(Ⅱ)若∠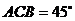 ,求△
,求△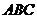 的外接圆的方程;
的外接圆的方程;
(Ⅲ)若在给定直线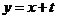 上任取一点
上任取一点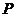 ,从点
,从点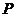 向(Ⅱ)中圆引一条切线,切点为
向(Ⅱ)中圆引一条切线,切点为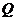 . 问是否存在一个定点
. 问是否存在一个定点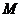 ,恒有
,恒有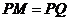 ?请说明理由.
?请说明理由.
17.(本小题满分14分)
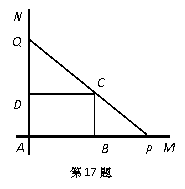
如图,互相垂直的两条公路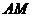 、
、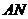 旁有一矩形花园
旁有一矩形花园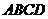 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园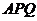 ,要求
,要求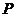 在射线
在射线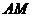 上,
上,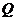 在射线
在射线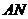 上,且
上,且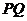 过点
过点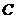 ,其中
,其中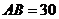 米,
米,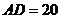 米. 记三角形花园
米. 记三角形花园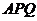 的面积为S.
的面积为S.
 (Ⅰ)当
(Ⅰ)当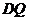 的长度是多少时,S最小?并求S的最小值.
的长度是多少时,S最小?并求S的最小值.
 (Ⅱ)要使S不小于
(Ⅱ)要使S不小于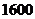 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?





16.(本小题满分14分) w ww.ks 5u.c o
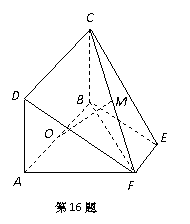 如图,等腰梯形
如图,等腰梯形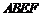 中,
中,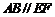 ,
,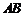 =2,
=2,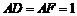 ,
,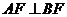 ,
,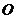 为
为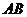 的中点,矩形
的中点,矩形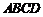 所在的平面和平面
所在的平面和平面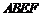 互相垂直.
互相垂直.
(Ⅰ)求证: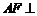 平面
平面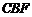 ;
;
(Ⅱ)设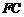 的中点为
的中点为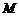 ,求证:
,求证: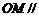 平面
平面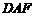 ;
;
(Ⅲ)求三棱锥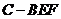 的体积.
的体积.
15.(本小题满分14分)
在△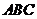 中,角
中,角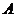 、
、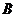 、
、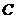 所对的边分别为
所对的边分别为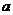 、
、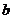 、
、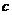 ,且
,且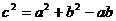 .
.
(Ⅰ)若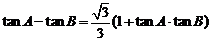 ,求角
,求角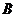 ;
;
(Ⅱ)设 ,
,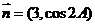 ,试求
,试求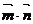 的最大值.
的最大值.
14.设函数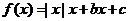 ,则下列命题中正确命题的序号有 ▲ . (请将你认为正确命题的序号都填上)
,则下列命题中正确命题的序号有 ▲ . (请将你认为正确命题的序号都填上)
①当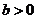 时,函数
时,函数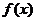 在R上是单调增函数; ②当
在R上是单调增函数; ②当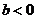 时,函数
时,函数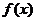 在R上有最小值;
在R上有最小值;
③函数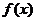 的图象关于点
的图象关于点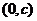 对称;
④方程
对称;
④方程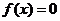 可能有三个实数根.
可能有三个实数根.
13.若二次函数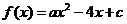 的值域为
的值域为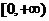 ,则
,则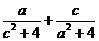 的最小值为 ▲ .
的最小值为 ▲ .
12.设等差数列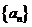 的首项及公差均是正整数,前
的首项及公差均是正整数,前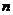 项和为
项和为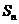 ,且
,且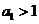 ,
,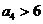 ,
,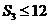 ,则
,则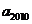
= ▲ .
10.已知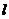 是一条直线,
是一条直线,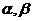 是两个不同的平面. 若从“①
是两个不同的平面. 若从“①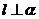 ;②
;②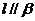 ;③
;③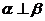 ”中选取两个作为条件,另一个作为结论,试写出一个你认为正确的命题 ▲ .(请用代号表示)
”中选取两个作为条件,另一个作为结论,试写出一个你认为正确的命题 ▲ .(请用代号表示)
9.中心在坐标原点,焦点在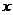 轴上的双曲线的一条渐近线方程为
轴上的双曲线的一条渐近线方程为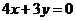 ,则该双曲线的离心率为 ▲ .
,则该双曲线的离心率为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com