

19.(本小题满分12分)
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①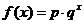 ;②
;②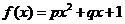 ;③
;③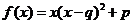 .(以上三式中、均为常数,且
.(以上三式中、均为常数,且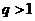 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(II)若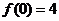 ,
,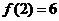 ,求出所选函数
,求出所选函数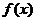 的解析式(注:函数定义域是
的解析式(注:函数定义域是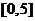 .其中
.其中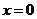 表示8月1日,
表示8月1日,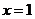 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
18.(本小题满分12分)
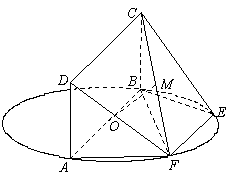
如图,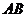 为圆
为圆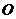 的直径,点、在圆
的直径,点、在圆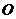 上,且
上,且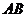 ∥
∥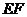 ,矩形
,矩形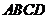 所在的平面和圆
所在的平面和圆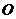 所在的平面互相垂直,且
所在的平面互相垂直,且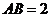 ,
,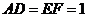 .
.
 (I)设
(I)设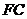 的中点为
的中点为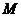 ,求证
,求证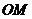 ∥平面
∥平面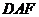 ;
;
(II)求直线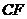 与平面
与平面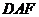 所成角的大小;
所成角的大小;
(III)求二面角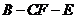 的余弦值.
的余弦值.
17.(本小题满分12分
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如图所示:
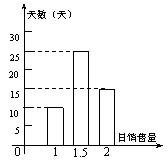 (I)计算这50天的日平均销售量;
(I)计算这50天的日平均销售量;
(II)若以频率作为概率,且每天的销售量相互独立.
①求5天中该种商品恰好有2天销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元,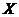 表示该种商品两天销售利润的和(单位:千元),求
表示该种商品两天销售利润的和(单位:千元),求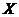 的分布列和数学期望.
的分布列和数学期望.
16. (本小题满分12分)
已知向量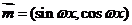 ,
,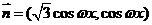 ,函数
,函数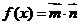 (
(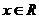 ,
,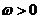 )的图象在轴右侧的第一个最高点的横坐标是
)的图象在轴右侧的第一个最高点的横坐标是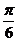 .
.
(I)求函数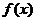 的解析式;
的解析式;
(II)若将函数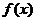 的图象向右平移
的图象向右平移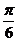 个单位后,再将得到的图象上所有的点横坐标伸长到原来的倍,纵坐标不变,得到
个单位后,再将得到的图象上所有的点横坐标伸长到原来的倍,纵坐标不变,得到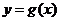 的图象,求函数
的图象,求函数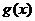 在区间
在区间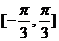 上的值域.
上的值域.
15. 已知椭圆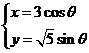 (
(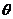 为参数)的左、右焦点分别为
为参数)的左、右焦点分别为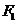 、
、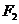 ,一直线经过右焦点
,一直线经过右焦点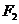 ,且与椭圆的长轴垂直,则在以原点为极点,轴正半轴为极轴的极坐标系中,该直线的极坐标方程为__________;若该直线与该极坐标系中的曲线
,且与椭圆的长轴垂直,则在以原点为极点,轴正半轴为极轴的极坐标系中,该直线的极坐标方程为__________;若该直线与该极坐标系中的曲线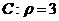 交于、两点,则
交于、两点,则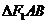 的面积为________.
的面积为________.
14. 已知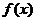 ,
,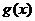 都是定义在上的函数,
都是定义在上的函数,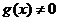 ,
,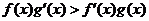 ,
,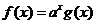 (
(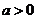 且
且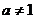 ),
),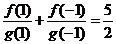 .对于有穷数列
.对于有穷数列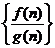 (
(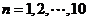 ),任取正整数
),任取正整数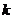 (≤
(≤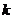 ≤
≤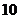 ),则前
),则前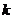 项和大于
项和大于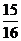 的概率是___________.
的概率是___________.
13. 在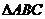 中,已知
中,已知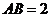 ,
,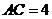 ,
,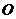 是
是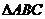 的外心.
的外心.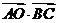 的值为_______.
的值为_______.
12.记等差数列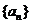 的前项和为
的前项和为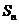 ,利用倒序相加法的求和办法,可将
,利用倒序相加法的求和办法,可将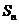 表示成首项
表示成首项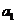 ,末项
,末项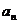 与项数的一个关系式,即
与项数的一个关系式,即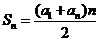 ;类似地,记等比数列
;类似地,记等比数列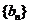 的前项积为
的前项积为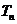 ,且
,且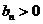 (
(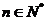 ),类比等差数列的求和方法,可将
),类比等差数列的求和方法,可将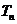 表示为首项
表示为首项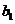 ,末项
,末项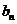 与项数的一个关系式,即公式
与项数的一个关系式,即公式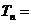 _________.
_________.
11. 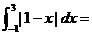 ____________.
____________.
10. 已知随机变量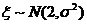 ,且
,且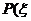 ≤
≤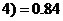 ,则
,则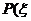 ≤
≤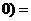 ___________
___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com