
3.函数 在
在 处的导数
处的导数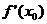 的几何意义:曲线
的几何意义:曲线 在其上点
在其上点 ,
, 处的切线的斜率。用导数研究切线问题,切点是关键(切点在切线上、切点在曲线上、切点横坐标的导函数值为切线斜率)。
处的切线的斜率。用导数研究切线问题,切点是关键(切点在切线上、切点在曲线上、切点横坐标的导函数值为切线斜率)。
[举例1]曲线 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A. B.
B. C.
C. D.
D. (07高考海南理10)
(07高考海南理10)
解析:

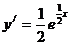 ,则]曲线在点
,则]曲线在点 处的切线斜率为:
处的切线斜率为: ,
,
∴切线方程为: ,它与坐标轴的交点分别为:(2,0),(0,-
,它与坐标轴的交点分别为:(2,0),(0,-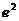 );
);
∴切线与坐标轴所围三角形的面积为: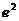 ,选D。
,选D。
[举例2]函数 的图象在点P处的切线方程是:
的图象在点P处的切线方程是: ,若点P的横坐标为5,
,若点P的横坐标为5,
则 =
。
=
。
解析:本题没有函数表达式,但有切线方程 ,注意到“切点在切线上”,
,注意到“切点在切线上”,
∴P(5,3);又“切点在曲线上”,∴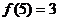 ;而曲线
;而曲线 在点P处的切线斜率为
在点P处的切线斜率为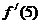 ,
,
即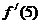 =-1,故
=-1,故 =2。
=2。
[举例3]已知直线 与抛物线
与抛物线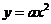 相切,则
相切,则
解析:本题固然可以将直线方程带入抛物线方程中,使得到的一元二次方程的判别式 =0,
=0,
从而求出 的值;但这种做法只限于二次曲线,若将抛物线换成其它的非二次曲线,则此路不通。以下用“导数”求解:“切点”是关键,记切点P(
的值;但这种做法只限于二次曲线,若将抛物线换成其它的非二次曲线,则此路不通。以下用“导数”求解:“切点”是关键,记切点P( ,
, ),
), ,则有:
,则有:
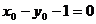 (切点在切线上)①;
(切点在切线上)①;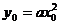 (切点在曲线上)②
(切点在曲线上)②
 =1 (切点横坐标的导函数值为切线斜率)③;由①②③解得:
=1 (切点横坐标的导函数值为切线斜率)③;由①②③解得: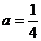 。
。
[巩固1]已知函数 的图象在点
的图象在点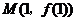 处的切线方程是
处的切线方程是 ,则
,则 ____.(07高考湖北文13)
____.(07高考湖北文13)
[巩固2]点P是曲线 上的动点,设点P处切线的倾斜角为
上的动点,设点P处切线的倾斜角为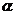 ,则
,则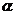 的取值范围是A、
的取值范围是A、 B、
B、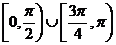 C、
C、 D、
D、
[巩固3]若直线y=x是曲线y=x3-3x2+ax的切线,则a=___________
2.常用导数公式: ,
, ,
, ,
, ;
;
导数的运算法则:若函数 与
与 的导数存在,则
的导数存在,则 ,
,
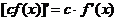 ,
, ;
;
 (这个公式很容易记错,注意和“积的导数”对比);
(这个公式很容易记错,注意和“积的导数”对比);
复合函数的导数:由 与
与 =
=
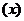 得到复合函数
得到复合函数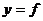
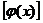 ,则
,则 =
= .
. 。
。
[举例1]已知 ,则
,则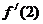 =
。
=
。
解析: 是常数,∴
是常数,∴

 =3+2
=3+2 -1
-1
 = -2
= -2
∴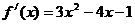 ,故
,故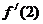 =3。
=3。
[举例2] ,
, =
。
=
。
解析:本题可以用“倒序相加”法,也可以用“通项变化”法(k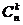 = n
= n );这里,我们观察
);这里,我们观察 ①,不难发现其通项
①,不难发现其通项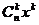 求导后的系数正是所求“项”;故考虑对①式两边同求导数,得:
求导后的系数正是所求“项”;故考虑对①式两边同求导数,得:
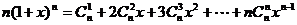 ,令
,令 =1得:
=1得:
 =
=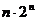
[巩固1] 已知 .令
.令 ,则
,则 = 。
= 。
[巩固2]已知函数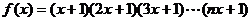 ,则
,则 的值为:
的值为:
A. B.
B. C.
C. D.
D.
1. 叫函数
叫函数 在
在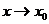 处的导数,记作
处的导数,记作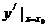 。
。
注:①函数应在点 的附近有定义,否则导数不存在。②在定义导数的极限式中,
的附近有定义,否则导数不存在。②在定义导数的极限式中,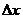 趋近于0可正、可负、但不为0,而
趋近于0可正、可负、但不为0,而 可能为0。③
可能为0。③ 是函数
是函数 对自变量
对自变量 在
在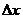 范围内的平均变化率,它的几何意义是过曲线
范围内的平均变化率,它的几何意义是过曲线 上点(
上点( ,
,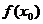 )及点(
)及点( +
+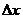 ,
,
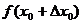 )的割线斜率。④导数
)的割线斜率。④导数 是函数
是函数 在点
在点 的处瞬时变化率,它反映的函数
的处瞬时变化率,它反映的函数 在
在 点处变化的快慢程度,它的几何意义是曲线
点处变化的快慢程度,它的几何意义是曲线 上点(
上点( ,
,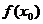 )处的切线的斜率。⑤若极限
)处的切线的斜率。⑤若极限 不存在,则称函数
不存在,则称函数 在点
在点 处不可导。⑥如果函数
处不可导。⑥如果函数 在开区间
在开区间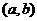 内每一点都有导数,则称函数
内每一点都有导数,则称函数 在开区间
在开区间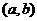 内可导;此时对于每一个
内可导;此时对于每一个 ∈
∈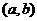 ,都对应着一个确定的导数
,都对应着一个确定的导数 ,从而构成了一个新的函数
,从而构成了一个新的函数 ,称这个函数
,称这个函数 为函数
为函数 在开区间
在开区间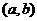 内的导函数,简称导数;导数与导函数都称为导数,这要加以区分:求一个函数的导数,就是求导函数;求一个函数在给定点的导数,就是求导函数值。
内的导函数,简称导数;导数与导函数都称为导数,这要加以区分:求一个函数的导数,就是求导函数;求一个函数在给定点的导数,就是求导函数值。
[举例1]若 ,则
,则 等于:
等于:
(A) -1 (B) -2 (C) 1 (D) 1/2
解析:∵ ,即
,即 =2
=2
 =-1。
=-1。
[举例2] 已知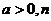 为正整数
为正整数 设
设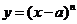 ,证明
,证明
解析:本题可以对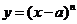 展开后“逐项”求导证明;这里用导数的定义证明:
展开后“逐项”求导证明;这里用导数的定义证明:
 =
=
 =
=
 =
=
 =
= 。
。
[巩固1]一质点作曲线运动,它的位移S与时间t的关系为: ,试用导数的定义求t =3时的速度。
,试用导数的定义求t =3时的速度。
[巩固2]设C是成本,q是产量,成本与产量的函数关系式为C=C(q),当产量为 时,产量变化
时,产量变化 对成本的影响可用增量比
对成本的影响可用增量比 刻划. 如果
刻划. 如果 无限趋近于0时,
无限趋近于0时, 无限趋近于常数A,经济学上称A为边际成本. 它表明当产量为
无限趋近于常数A,经济学上称A为边际成本. 它表明当产量为 时,增加单位产量需付出成本A(这是实际付出成本的一个近似值)。设生产x个单位产品的总成本函数是C(x)=8+
时,增加单位产量需付出成本A(这是实际付出成本的一个近似值)。设生产x个单位产品的总成本函数是C(x)=8+ ,则生产8个单位产品时,边际成本是: ( )
,则生产8个单位产品时,边际成本是: ( )
A.2 B.8 C.10 D.16
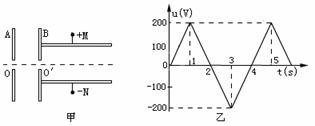
12.如图(甲)所示,A、B为两块距离很近的平行金属板(电子通过A、B间的时间可忽略不计),板中央均有小孔。一束电子以初动能EKO=120eV,从A板上的小孔O不断垂直于板射入A、B之间,在B板右侧,平行金属板M、N之间有匀强电场,板长L=2×10-2m,板间距离d=4×10-3m;偏转电压U=20V,现在A、B间加一个如图(乙)变化的电压,在t=0到t=2s时间内,A板的电势高于B板的电势,则在U随时间变化的第一个周期时间内:
⑴电子在哪段时间内可以从B板上的小孔O'射出?
⑵在哪段时间内,电子能从偏转电场右侧飞出?
11.用轻弹簧相连的质量均为2 kg的A、B两物块都以v=6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量4 kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动.求:在以后的运动中:
(1)当弹簧的弹性势能第一次达到最大时,物体A的速度多大?弹性势能的最大值是多大?
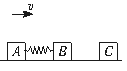 (2)A的速度有可能向左吗?为什么?
(2)A的速度有可能向左吗?为什么?
10.下图是过山车的模型图,在图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为α=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接。现使小车(视作质点)从P点以一定的初速度沿斜面向下运动。已知斜轨道面与小车间的动摩擦因数为μ=1/24,g=10m/s2,sin37°=0.6,cos37°=0.8。问:
⑴若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
⑵若小车在P点的初速度为10m/s,则小车能否安全通过两个圆形轨道?

9.(1)螺旋测微器的测量结果是: cm

 (2)一只电压表的量程是3.0V,其内阻RV 约900Ω。某同学用如图所示的电路来测定RV 的准确值,实验步骤如下:
(2)一只电压表的量程是3.0V,其内阻RV 约900Ω。某同学用如图所示的电路来测定RV 的准确值,实验步骤如下:
①按图正确连接电路,将滑动变阻器R1的滑片移到最右端,将电阻箱R的阻值调到最大值。
②闭合电键S1、S2,调节R1的阻值,使电压表指针指到满偏。
③保持S1闭合,断开S2,调节R和R1的阻值,使电压表指针指到满偏的一半。
④读出电阻箱的阻值,即为电压表的内阻。
 ⑴在该实验中,有两个滑动变阻器可供选择:a:最大阻值为2000Ω,额定电流为1A;b:最大阻值为20Ω,额定电流为2A。根据实验电路的实际情况,应选用其中的_______。
⑴在该实验中,有两个滑动变阻器可供选择:a:最大阻值为2000Ω,额定电流为1A;b:最大阻值为20Ω,额定电流为2A。根据实验电路的实际情况,应选用其中的_______。
⑵上述实验步骤中有一步里有重大错误,这一步是第 步,请你把正确的操作写在下面:
。
⑶该实验存在系统误差。设RV 的测量值和真实值分别为R测和R真,则应该有R测_____R真(填大于、小于或等于)。
⑷用笔画线当导线,将右边的实验器材按照电路图连成实验电路。
8. 如图8所示,平行板电容器AB两极板水平放置,A在上方,B在下方,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性,一带电小球沿AB 中心水平射入,打在B极板上的N点,小球的重力不能忽略,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是 ( )
如图8所示,平行板电容器AB两极板水平放置,A在上方,B在下方,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性,一带电小球沿AB 中心水平射入,打在B极板上的N点,小球的重力不能忽略,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是 ( )
A.若小球带正电,当A B间距增大时,小球打在N的右侧
B.若小球带正电,当A B间距减小时,小球打在N的左侧
C.若小球带负电,当A B间距减小时,小球可能打在N的右侧
D.若小球带负电,当A B间距增大时,小球可能打在N的左侧
 2009-2010学年高三月考物理试题答卷纸
2009-2010学年高三月考物理试题答卷纸
7. 如图所示,空间有与水平方向成θ角的匀强电场。一个质量为m的带电小球,用长L的绝缘细线悬挂于O点。当小球静止时,细线恰好处于水平位置。现用一个外力将小球沿圆弧缓慢地拉到最低点,此过程小球的电荷量不变。则该外力做的功为( )
如图所示,空间有与水平方向成θ角的匀强电场。一个质量为m的带电小球,用长L的绝缘细线悬挂于O点。当小球静止时,细线恰好处于水平位置。现用一个外力将小球沿圆弧缓慢地拉到最低点,此过程小球的电荷量不变。则该外力做的功为( )
A.mgL B.mgL tanθ C.mgLcotθ D.mgL/cosθ
6.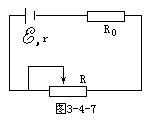 如图所示,电源电动势
如图所示,电源电动势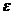 =5V,内阻r=10Ω,R0=90Ω,R为滑动变阻器,最大阻值为400Ω,以下说法正确的是( )
=5V,内阻r=10Ω,R0=90Ω,R为滑动变阻器,最大阻值为400Ω,以下说法正确的是( )
A.R的阻值为80时,R0消耗的电功率最大
B.R的阻值为400Ω时,电源的路端电压最大
C.R的阻值为100Ω时,R消耗的电功率最大
D.R0上消耗的电功率最小值是9×10-2W
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com