20．已知正数列的前n项和

　 (I)求的通项公式；

　 (II)令，问数列的前多少项的和最大？

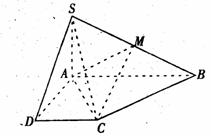
19．如图已知四棱锥S-ABCD的底面是直角梯形，AB//DC，，底面

ABCD，且SA=AD=DC=是SB的中点。

　 　 (1)证明：平面平面SCD；

　 (2)求AC与SB所成的角；

　 (3)求二面角M-AC-B的大小。

18．已知将一枚残缺不均匀的硬币连抛三次落在平地上，三次都正面朝上的概率为。

　 (1)求将这枚硬币连抛三次，恰有两次正面朝上的概率；

　 (2)若甲将这枚硬币连抛三次之后，乙另抛一枚质地均匀的硬币两次。若正面朝上的总次数多者为胜者，求甲获胜的概率？

17．已知的周长为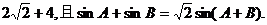

　 (1)求边AB的长；

　 (2)若的面积，求角C的大小。

16．已知正三棱锥S-ABC内接于一个半径为6的球，

过侧棱SA及球心O的平面截三棱锥及球面所得

的截面图如右图所示，则此三棱锥的一个侧面

的面积为　　　　 。

14．函数的定义域为　　　　　　　 。

　 15．经过抛物线的焦点F，作倾斜角45°的射

线与抛物线交于A点，则|FA|=　　　 。

13．二项式的展开式中常数项是　　　　　　　 .

12．已知函数，则使M=N成立的实数对(a，b)有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　　 A．2对　　　　　　　　　　　　　 B．3对　　　　　　　　　　　　　 C．4对　　　　　　　　　　　　　 D．5对

第Ⅱ卷 　非选择题(共90分)

11．实数x，y满足条件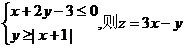的最小值是　　　　　　　　　　　　　　　　　 (　　 )

A．-19　　　　　　　　　　　　　　 B．-5　　　　　　　　　　　　　　　 C．-　　　　　　　　　　　　　　 D．0

10．已知、双曲线和抛物线的离心率分别为，则下列关系不正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　　 A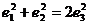．　　 B．　　　　　　　 C．　　　　　　　 D．