
3.2010年2月28日以后三天四川、云南、广西依
旧以晴天为主,原因是 ( )
A.寒潮过境,天气晴朗
B.受西伯:利亚、蒙古高压控制
C.冷锋锋前无降水
D.当地空气中水汽含量少
2.下列关于温哥华附近地区自然地理现象说法正确的是 ( )
A.冬季气候寒冷河流结冰期长
B.降水主要来自北太平洋暖湿气流
C.河流径流季节变化大
D.沿岸寒流使冬季天气更加寒冷
 今年1月以来,新疆连续遭受强冷空气袭击,部分
今年1月以来,新疆连续遭受强冷空气袭击,部分
地区出现严重寒潮暴雪灾害,给群众生活、交通运输、
农牧业以及旅游业带来巨大影响。
2009年秋季以来,云南温高雨少,出现特大干旱。
进入2010年,干旱迅速发展蔓延,贵州、广西、四川、
重庆、山西、河南、陕西等地也出现不同程度的干旱。
特别是云南、广西等主旱区的旱情呈发展态势。
读图l“2010年2月28日地面天气形势图”,
回答3-5题。
1.温哥华冬奥会开幕时 ( )
A.日本东京正烈日炎炎
B.智利圣地亚哥正旭日东升
C.美国纽约正夕阳西下
D.英国伦敦正处在深夜
2010.4
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共300分。考试时间150分钟。考试结束,将本试卷和答题卡一并收回。
第Ⅰ卷(选择题共140分)
本卷共35小题,每小题4分,共140分。在每小题列出的四个选项中。选出最符合题
目要求的一项。
当地时间2月12日18时(区时),第21届冬奥会在温哥华(北纬49°16′,西经123°7′)哥伦比亚体育馆拉开帷幕。温哥华是加拿大西岸最大的港口。回答l、2题。
20.(本小题共14分)
数列 的前n项和为
的前n项和为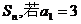 ,点
,点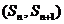 在直线
在直线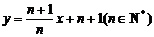
上.
(I)求证:数列 是等差数列;
是等差数列;
(II)若数列 满足
满足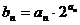 ,求数列
,求数列 的前n项和
的前n项和
(III)设 ,求证:
,求证: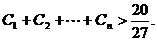
19.(本小题共14分)
已知椭圆的中点在原点O,焦点在x轴上,点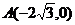 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且
(I)求椭圆的方程;
(II)若平行于CO的直线 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
18.(本小题共13分)
已知函数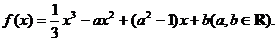
(I)若x=1为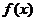 的极值点,求a的值;
的极值点,求a的值;
(II)若 的图象在点(1,
的图象在点(1, )处的切线方程为
)处的切线方程为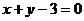 ,求
,求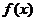 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(III)当 时,若
时,若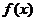 在区间(-1,1)上不单调,求a的取值范围.
在区间(-1,1)上不单调,求a的取值范围.
17.(本小题共13分)
某校高三年级有男生105人,女生126人,教师42人,用分层抽样的方法从中抽取13人,进行问卷调查.设其中某项问题的选择支为“同意”,“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
|
|
同意 |
不同意 |
合计 |
|
教师 |
1 |
|
|
|
女生 |
|
4 |
|
|
男生 |
|
2 |
|
(I)请完成此统计表;
(II)试估计高三年级学生“同意”的人数;
(III)从被调查的女生中选取2人进行访谈,求选到的两名学生中,恰有一人“同意”一人“不同决的概率.”
16.(本小题共13分)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
 (I)求证:PE⊥BC;
(I)求证:PE⊥BC;
(II)求证:EF//平面PAD.
15.(本小题共13分)
已知函数
(I)当a=1时,求函数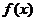 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;
(II)当a=2时,在 的条件下,求
的条件下,求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com