1．已知等差数列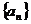满足则有　　　　　 ( 　　)

A.　 　　　B.　 　　C. 　　　　D.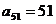

2在正数等比数列中已知 　则 ( 　　)

A．11　　　　　　　　　 B．10　　　　　　　 C．8　　　　　　　　 D．4

3．例3是比较简单的数列应用问题，由于问题所涉及的数列是熟悉的等比数列与等差数列，因此只建立通项公式并运用所学过的公式求解.

冲刺强化训练(14)

班级＿＿＿＿＿　姓名＿＿＿＿＿　学号＿＿＿＿＿　　　　　　 日期＿＿月＿＿日

2．数列通项公式和递推公式经常在已知条件中给出,利用列举、叠加、叠乘等方法求之.求通项公式的方法应掌握.

1．本题的关键在于指数式和对数式的互化在数列中的应用。

3、某企业进行技术改造，有两种方案，甲方案：一次性贷款10万元，第一年便可获利1万元，以后每年比前一年增加30%的利润；乙方案：每年贷款1万元，第一年可获利1万元，以后每年比前一年增加5千元；两种方案的使用期都是10年，到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算，试比较两种方案中，哪种获利更多？

(取)

[方法点拨]

2、设数列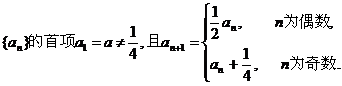

记　　 　　　　　　　　　　　　　　

　 (Ⅰ)求a₂，a₃；

　 (Ⅱ)判断数列是否为等比数列，并证明你的结论；

1、已知数列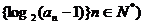为等差数列，且　　　　　　 (05湖南)

　 (Ⅰ)求数列的通项公式；(Ⅱ)证明

5. (2005年杭州二模题)已知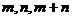成等差数列,成等比数列,则椭圆的准线方程为 _______　　　 _ .

[例题探究]

4．已知等差数列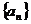的公差为2,若成等比数列, 则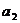= (　　 )(浙江文理)

A　 –4　　 　　　　　　　　　 B　 –6 　　　　　　　　　　　　 C　 –8　 　　　　　　　　　　　　　 　D　 –10

3．设S_n是等差数列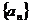的前n项和，若　　 (　　 )(福建文)

A．1　　　　　　　　　　　　　　 B．－1　　　　　　　　　　　　　　 C．2　　　　　　　　　　　　　　　　 D．