
1. 函数自身的对称性探究
高考题回放:(2005年广东卷I)设函数
 ,
, ,且在闭区间[0,7]上只有
,且在闭区间[0,7]上只有
(1)试判断函数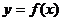 的奇偶性;
的奇偶性;
(2)试求方程 在闭区间[-2005,2005]上根的个数并证明你的结论。
在闭区间[-2005,2005]上根的个数并证明你的结论。
分析:由 可得:函数图象既关于x=2对称,又关于x=7对称,进而可得到周期性,然后再继续求解,而本题关键是要首先明确函数的对称性,因此,熟悉函数对称性是解决本题的第一步。
可得:函数图象既关于x=2对称,又关于x=7对称,进而可得到周期性,然后再继续求解,而本题关键是要首先明确函数的对称性,因此,熟悉函数对称性是解决本题的第一步。
定理1 函数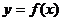 的图像关于直线x=a对称的充要条件是
的图像关于直线x=a对称的充要条件是 即
即
证明(略)
推论 函数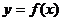 的图像关于y轴对称的充要条件是
的图像关于y轴对称的充要条件是
定理2 函数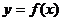 的图像关于点A(a,b)对称的充要条件是
的图像关于点A(a,b)对称的充要条件是

证明(略)
推论 函数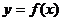 的图像关于原点O对称的充要条件是
的图像关于原点O对称的充要条件是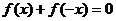
偶函数、奇函数分别是定理1,定理2的特例。
定理3 ①若函数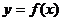 的图像同时关于点A(a,c)和点B(b,c)成中心对称(
的图像同时关于点A(a,c)和点B(b,c)成中心对称( ),则
),则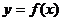 是周期函数,且
是周期函数,且 是其一个周期。
是其一个周期。
②若函数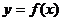 的图像同时关于直线
的图像同时关于直线 成轴对称(
成轴对称( ),则
),则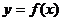 是周期函数,且
是周期函数,且 是其一个周期。
是其一个周期。
③若函数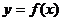 的图像既关于点A(a,c)成中心对称又关于直线x=b成轴对称(
的图像既关于点A(a,c)成中心对称又关于直线x=b成轴对称( ),则
),则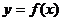 是周期函数,且
是周期函数,且 是其一个周期。
是其一个周期。
以下给出③的证明,①②的证明留给读者。
因为函数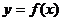 的图像关于点A(a,c)成中心对称。
的图像关于点A(a,c)成中心对称。
所以 代
代 得:
得:

又因为函数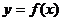 的图像关于直线
的图像关于直线 成轴对称。
成轴对称。
所以 代入(*)得:
代入(*)得:
 得
得
 代入(**)得:
代入(**)得:
 是周期函数,且
是周期函数,且 是其一个周期。
是其一个周期。
例8. 已知函数 是奇函数,当x>0时,f(x)有最小值2,其中
是奇函数,当x>0时,f(x)有最小值2,其中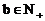 ,且
,且
(1)试求f(x)的解析式;
(2)问函数f(x)的图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由。
解:知函数 是奇函数,
是奇函数, ,则c=0
,则c=0
由于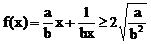 ,所以
,所以 ,又
,又 ,又
,又 ,于是
,于是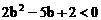
解得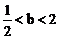 ,又
,又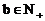
所以b=1,a=1
所以
(2)设点(x0,y0)存在关于点(1,0)对称点( ,y0),此两点均在函数
,y0),此两点均在函数 的图象上,则
的图象上,则
联立以上两式得 ,即
,即 ,从而,当
,从而,当 时,得
时,得 ;当
;当 时,得
时,得
即存在点( ),(
),( )关于点(1,0)对称。
)关于点(1,0)对称。
湖南省永州市第一中学(425006)
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
函数奇偶性的性质及其应用 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
函数奇偶性的性质及其应用 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩秋荣 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
例7. 若 ,求
,求 的值。
的值。
解:设 ,则f(x)是偶函数
,则f(x)是偶函数
则 的奇数次方的系数
的奇数次方的系数

则
例5. 解不等式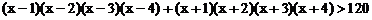
解:设 ,因
,因 ,则f(x)是偶函数,即f(x)的奇数次方为0,可设
,则f(x)是偶函数,即f(x)的奇数次方为0,可设 ,以x=1代入,得
,以x=1代入,得

解得A=70,即 ,原不等式可化为:
,原不等式可化为:

即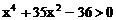
即
因而 或x>1
或x>1
例6. (2004年上海卷)设奇函数f(x)的定义域是[-5,5]。当 时,f(x)的图象如图1,则不等式f(x)<0的解是______________。
时,f(x)的图象如图1,则不等式f(x)<0的解是______________。

图1
解:根据奇函数图象关于原点成中心对称的性质,画出函数 在区间[-5,5]上的图象如图2,易知不等式
在区间[-5,5]上的图象如图2,易知不等式 的解是
的解是 。
。

图2
例3. 设f(x)是定义在R上的奇函数,当x>0时,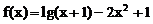 。试求此函数的解析式。
。试求此函数的解析式。
解:(1)当x=0时, ,于是
,于是 ;
;
(2)当x<0时, ,则
,则 ,由于f(x)是定义在R上的奇函数,则
,由于f(x)是定义在R上的奇函数,则

此函数的解析式为

例4. 设 ,f(x)是奇函数,g(x)是偶函数,
,f(x)是奇函数,g(x)是偶函数, ,求f(x)的表示式。
,求f(x)的表示式。
解:f(x)是奇函数,有 ;g(x)是偶函数,有
;g(x)是偶函数,有 ,则
,则

即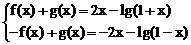
两式相减得
例3. 设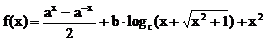 (其中a,b,c为常数),且
(其中a,b,c为常数),且 ,试求f(2)的值。
,试求f(2)的值。
解:设 ,易证g(x)是奇函数,故
,易证g(x)是奇函数,故
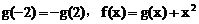
于是
两式相加得: ,即
,即
例1. 判定函数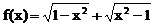 的奇偶性。
的奇偶性。
解:函数的定义域满足 ,即为
,即为 ,函数的图象表示两个点:(-1,0),(1,0)。其图象既关于原点对称,又关于y轴对称。从而函数f(x)既是奇函数又是偶函数。
,函数的图象表示两个点:(-1,0),(1,0)。其图象既关于原点对称,又关于y轴对称。从而函数f(x)既是奇函数又是偶函数。
5. 数形结合
数形结合是寻找解题切入点的一条重要途径,它是把已知或要求的式子与图形结合起来。应用数形结合思想,就是充分考查数学问题的条件和结论之间的内在联系,既分析其代数意义又揭示其几何意义,将数量关系和空间形式巧妙结合,来寻找解题思路,使问题得到解决。运用这一数学思想,要熟练掌握一些概念和运算的几何意义及常见曲线的代数特征。
例6. 已知 (其中
(其中 ),且
),且 是方程
是方程 的两根(
的两根( ),则实数a、b、
),则实数a、b、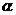 、
、 的大小关系为( )
的大小关系为( )
A.  B.
B.

C.  D.
D.

解析:a,b是方程 的两根,在同一坐标系中作出函数
的两根,在同一坐标系中作出函数 的图象如图所示:
的图象如图所示:

答案:A
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
再谈解题切入点的找寻 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
再谈解题切入点的找寻 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
张玲 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
4. 把握转化
化归与转化的思想方法无处不在,它是寻求问题解决过程中最重要、最活跃的一个环节,是分析、解决问题的有效途径,是数学中最基本、最常用、最重要的思想方法,也是寻找解题切入点的常用方法。
例5. 两条异面直线称为“一对”,则在正方体八个顶点间的所有连线中,成异面直线的共有多少对?
分析:如果以其中一条棱进行分类的话,很难搞清“重”和“漏”,然而我们对以下两题很熟悉:①以正方体的八个顶点为顶点的三棱锥有多少?②如果两条异面直线称为“一对”的话,一个三棱锥中有多少对异面直线?故可把本题分解成两个熟悉的问题,即考虑一种对应,由于①的答案是 个;②的答案是3对,故本题答案为
个;②的答案是3对,故本题答案为 对。
对。
点评:若直接寻找异面直线的对数很繁且易漏,而引入三棱锥通过计算三棱锥的个数,使得三棱锥的个数与异面直线的对数建立了一个对应,从而使问题转化为我们所熟悉的问题。
3. 展开联想
对于某些数学问题,从结构上的特点出发,在寻求命题的条件和结论间的逻辑联系时,由此及彼地联想(联想定义、定理或解决过的类似问题等),常常能启发思维,找到解题的切入点。
例4. 已知 是定义在R上的函数,且
是定义在R上的函数,且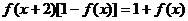 ,
, ,
,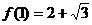 ,求
,求 的值。
的值。
分析:由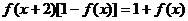 且
且 ,
,
 联想到三角公式
联想到三角公式
 。由
。由 的周期为
的周期为
 ,猜想可能为周期函数,
,猜想可能为周期函数, 是它的一个周期。
是它的一个周期。
解:


因此 是以8为周期的周期函数。
是以8为周期的周期函数。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com