
例2. 求值:
解:如图2,将边长为1的正七边形ABCDEFO放进直角坐标系中,则 ,
,

图2
又

又

例1. 用向量法证明:直径所对的圆周角是直角。
已知:如图1,AB是⊙O的直径,点P是⊙O上任一点(不与A、B重合),求证:∠APB=90°。

图1
证明:联结OP,设向量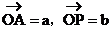 ,则
,则 且
且 ,
,
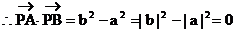
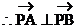 ,即∠APB=90°。
,即∠APB=90°。
例6. 求 在
在 上的极值。
上的极值。
错解:由题意得
令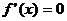 ,得
,得
当 时,
时, 在
在 附近两侧的符号相反,左正右负
附近两侧的符号相反,左正右负
∴ ,是函数的极大值点。
,是函数的极大值点。
剖析:错误的主要原因是解题过程中忽略了对函数的不可导点的考察,因为函数的极值可以在定义域内导数为零的点或不可导点取得。所以后面还应该加上:在定义域内不可导的点为:
经计算, 在
在 附近两侧的符号相反,左负右正
附近两侧的符号相反,左负右正
 在
在 附近两侧的符号相反,左负右正
附近两侧的符号相反,左负右正
 和
和 是函数的两个极小值点
是函数的两个极小值点
∴函数的极大值为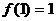
极小值为
(函数的图象见上图)
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
导数的应用典型错误解析 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
导数的应用典型错误解析 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
李红英 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
例5. 求 在
在 上的最大值和最小值。
上的最大值和最小值。
错解:由题意得
令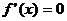 得
得

∴当 和3时,函数的最大值是
和3时,函数的最大值是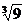
当 时,函数的最小值是1
时,函数的最小值是1
剖析:错误的主要原因是解题过程中忽略了对函数的不可导点的考察,因为函数的最值可以在导数为零的点或不可导点或区间的端点处取得。所以后面应该加上:在定义域内不可导的点为:

∴当 和3时,函数的最大值是
和3时,函数的最大值是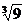
当 或2时,函数的最小值是0
或2时,函数的最小值是0
函数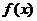 的图象如图
的图象如图

例4. 已知函数 在
在 内单调递减,求实数a的取值范围。
内单调递减,求实数a的取值范围。
错解: ,由函数
,由函数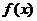 在
在 内单调递减知
内单调递减知 在
在 内恒成立
内恒成立
即 在
在 内恒成立
内恒成立
因此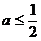
剖析:错误的主要原因是由于对函数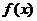 在D上单调递增(或递减)的充要条件是
在D上单调递增(或递减)的充要条件是 (或
(或 )且
)且 在D任一子区间上不恒为零没有理解。而当
在D任一子区间上不恒为零没有理解。而当 时
时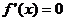 在
在 恒成立,所以不符合题意,舍去。
恒成立,所以不符合题意,舍去。
例3. 求函数 的单调增区间。
的单调增区间。
错解:由题意得

又因为函数的定义域是
所以函数的单调递增区间是(0,1)和(1, )。
)。
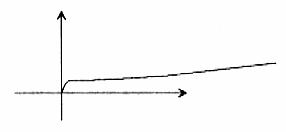
剖析:错解错在对函数在 处是否连续没有研究,显然函数在
处是否连续没有研究,显然函数在 处是连续的,所以函数的单调递增区间是
处是连续的,所以函数的单调递增区间是 。(函数的图象见下图)对于
。(函数的图象见下图)对于 (或
(或 )的解集中的断开点的连续性,我们要进行研究,不能草率下结论。
)的解集中的断开点的连续性,我们要进行研究,不能草率下结论。
例2. 函数 在
在 处有极值10,求a、b的值。
处有极值10,求a、b的值。
错解: ,由题意知
,由题意知
 ,且
,且
即 ,且
,且
解之得 或
或
剖析:错误的主要原因是把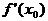 为极值的必要条件当作了充要条件,
为极值的必要条件当作了充要条件,
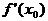 为极值的充要条件是
为极值的充要条件是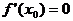
且 附近两侧的符号相反,所以后面应该加上:
附近两侧的符号相反,所以后面应该加上:
当 时
时
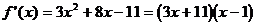
在 附近两侧的符号相反,
附近两侧的符号相反,
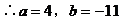
当 时,
时,
在 附近两侧的符号相同,
附近两侧的符号相同,
所以 舍去。
舍去。
∴( 时,
时,
 的图象见下面左图,
的图象见下面左图,
 时,
时,
 的图象见下面右图。)
的图象见下面右图。)

例1. 已知函数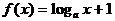 ,求
,求
错解:因为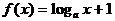


剖析:错误的主要原因是由于对导数的定义理解不清,导数
函数在某一点 处的导数,就是函数在这一点的函数值的增量与自变量的增量的比值在自变量的增量趋近于零时的极限,分子分母中的自变量的增量△x必须保持对应一致,它是非零的变量,它可以是
处的导数,就是函数在这一点的函数值的增量与自变量的增量的比值在自变量的增量趋近于零时的极限,分子分母中的自变量的增量△x必须保持对应一致,它是非零的变量,它可以是 ,
, 等。
等。

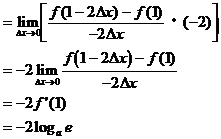
2. 求函数 的最大值。
的最大值。
例5 已知二次函数 满足条件
满足条件 ,
, ,且方程
,且方程 有两个相等实根。问是否存在实数
有两个相等实根。问是否存在实数 ,使得
,使得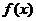 的定义域为[m,n]时,值域为[3m,3n]。如果存在,求出m、n的值;如果不存在,请说明理由。
的定义域为[m,n]时,值域为[3m,3n]。如果存在,求出m、n的值;如果不存在,请说明理由。
解:因 ,所以函数
,所以函数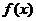 的图象的对称轴为直线
的图象的对称轴为直线
 =1,可得
=1,可得 ①
①
由 ,得
,得 ②
②
因方程 有两个相等实根,即
有两个相等实根,即 有相等实根,所以
有相等实根,所以 ③
③
将①代入②,得 。由③知,b=1,所以
。由③知,b=1,所以 。
。
则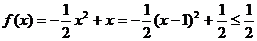 ,
,
所以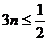 ,即
,即 。
。
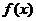 在[m,n]上单调递增,假设存在满足条件的m、n,则
在[m,n]上单调递增,假设存在满足条件的m、n,则

解得
又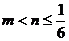 ,则m=-4,n=0,即存在m=-4,n=0满足条件。
,则m=-4,n=0,即存在m=-4,n=0满足条件。
注:解决定义域和值域共存问题时,不要盲目进行分类讨论,而应从条件出发,分析和探讨出解决问题的途径,确定函数的单调性,从而使问题得以解决。
练一练:
1. 求下列函数的值域:
① ;②
;② ;③
;③ 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com