
例5. 在100件产品中,有98件合格品,2件次品,从这100件产品中任意抽出3件,至少有1件次品的抽法有多少种?
分析:抽出3件,至少有1件次品的抽法的种数,就是从100件中抽出3件的抽法总数减去3件都是合格品的抽法的种数,即: (种)。
(种)。
注意:所有问题的解决都是分类或分步进行的,只不过排列、组合把一些程序化的步骤简化成一步,因此,两个原理贯穿本章始终。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
正确理解和使用两个原理 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
正确理解和使用两个原理 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩秋荣 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
例4. 同班4人各写1张贺年卡,先集中起来,然后每人从中各拿1张恰好是别人送出的贺年卡,则4张贺年卡不同的分配方式有( )
A. 6种 B. 9种 C. 11种 D. 23种
分析:设4人为甲、乙、丙、丁,则甲送出的卡片可以且只可以由其他三人中的一人收到,故有3种分配方式。以乙收到为例,其他人收到卡片的情况可分为两类:第一类,甲收到乙送出的卡片,这时丙、丁只有互送卡片1种分配方式;第二类,甲收到的不是乙送出的卡片,这时,甲收到卡片的方式有2种(分别是丙或丁送出的),对每一种情况,丙、丁收到卡片的方式只有1种。因此,根据分步计数原理,不同的分配方式有:3×(1+2)=9(种)。
注意:解题的关键在第2个人和第3个人的拿法,只要给他们规定一个拿卡的顺序,依次进行,则根据分步计数原理即可求得,也可画示意图帮助思考。
例2. 某艺术小组有9人,每人至少会钢琴和小号中的1种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴和会小号的各1人,有多少种不同的选法?
分析:由题意知,在艺术小组9人中,有且仅有1人既会钢琴又会小号(称为“多面手”),只会钢琴的有6人,只会小号的有2人。把“多面手”的选法分为两类:
(1)“多面手”入选,则有8种选法;
(2)“多面手”不入选,则选法有:6×2=12(种)
因此选法共有:8+6×2=20(种)
注意:像本题中的“多面手”可称为“特殊对象”,在解题中按“特殊对象”进行分类是常用的方法,要注意分类的独立性。在综合运用两个原理时,既要会合理分类,又要会合理分类,一般是先分类,后分步。
例3. 用6种不同的颜色为广告牌着色,要求在①、②、③、④四个区域中相邻的区域用不同的颜色,共有多少种不同的着色方法?

分析:完成着色这件事,共分四个步骤,为①着色有6种方法,为②着色有5种方法,为③着色有4种方法,为④着色也有4种方法,故着色方法共有:6×5×4×4=480(种)
注意:解这种问题应注意分步的连续性,必要时,分步中再分类。
例1. 一个口袋里有5封信,另一个口袋里有4封信,各封信内容均不相同。
(1)从两个口袋里,各取1封信,有多少种不同的取法?
(2)从两个口袋里,任取1封信,有多少种不同的取法?
(3)把这两个口袋里的9封信,分别投入4个邮筒,有多少种不同的放法?
分析:(1)各取1封信,无论从哪个口袋里取,都不能算完成了这件事,因此应分两个步骤完成。由分步计数原理知,取法有:5×4=20(种)。
(2)任取1封信,无论从哪个口袋里取,都能单独完成这件事,因此有两类办法。由分类计数原理知,取法共有:5+4=9(种)。
(3)从每封信投入邮筒的可能性考虑,第1封信投入邮筒有4种可能,第2封信仍有4种可能,…,第9封信仍有4种可能。由分步计数原理可知,共有49种不同的放法。
例3. 从10件产品(其中次品有3件)中,一件一件不放回地任意取出4件,求4件中恰有1件次品的概率。
错误:因为第一次有10种取法,第二次有9种取法,第三次有8种取法,第四次有7种取法,由乘法原理可知,从10件取4件共有10×9×8×7种取法。
设A=“取出的4件中恰有1件次品”,则A含有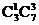 种取法(先从3件次品中取1件,再从7件正品中取3件)。
种取法(先从3件次品中取1件,再从7件正品中取3件)。
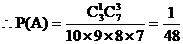
剖析:计算基本事件的个数是用排列的方法,即考虑了抽取的顺序;而计算事件A所包含的基本事件的个数时是用组合的方法,即没有考虑抽取的顺序。
正解:(1)都用排列方法。
从10件产品中取4件共含有 个基本事件,A包含
个基本事件,A包含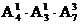 个基本事件(4件中要恰有1件次品,可以看成四次抽取中有一次抽到奖品,有
个基本事件(4件中要恰有1件次品,可以看成四次抽取中有一次抽到奖品,有 种方式,对于每一方式,从3件次品中取一件,再从7件正品中一件一件地取3件,共有
种方式,对于每一方式,从3件次品中取一件,再从7件正品中一件一件地取3件,共有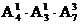 种取法)。
种取法)。
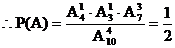
(2)都用组合方法
一件一件不放回地抽取4件,可以看成一次抽取4件,故共含有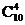 个基本事件,A包含有
个基本事件,A包含有 个基本事件。
个基本事件。

|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
概率问题中的对比思考 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
概率问题中的对比思考 |
栏目名称 |
学法指导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
许咏梅 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
例2. 从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A. 至少有1个白球,都是白球
B. 至少有1个白球,至少有1个红球
C. 恰有1个白球,恰有2个白球
D. 至少有1个白球,都是红球
错解:选D
剖析:本题错误的原因在于把“互斥”与“对立”混同,要准确解答这类问题,必须搞清对立事件与互斥事件的联系与区别,这二者的联系与区别主要体现在以下三个方面:
(1)两事件对立,必定互斥,但互斥未必对立;
(2)互斥的概念适用于多个事件,但对立的概念只适用于两个事件;
(3)两个事件互斥只表明这两个事件不能同时发生,即至多只能发生其中一个,但可以都不发生;而两事件对立则表示它们有且仅有一个发生。
正解:A、B不互斥,当然也不对立,C互斥而不对立,D不但互斥而且对立,所以正确答案应为C。
例1. 先后抛掷两枚骰子,求事件A:出现的点数之和等于3的概率。
错解:掷两枚骰子出现的点数之和的可能数值为{2,3,4,……,12},事件A的结果只有3,故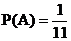
剖析:公式P(A)= 仅当所述的试验结果是等可能时才成立,而取数值2和3不是等可能的,2只有1种情况(1,1)出现,而3有两种情况(1,2),(2,1)可出现,其他的情况可类推。
仅当所述的试验结果是等可能时才成立,而取数值2和3不是等可能的,2只有1种情况(1,1)出现,而3有两种情况(1,2),(2,1)可出现,其他的情况可类推。
正解:先后抛掷两枚骰子可能出现的情况有:(1,1),(1,2),……,(1,6),(2,1),(2,2),……,(2,6),……,(6,1),(6,2),……,(6,6),基本事件总数为6×6=36
在这些结果中,事件A只有两种结果(1,2),(2,1)
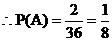
例4 椭圆 与x轴的正向相交于点A,O为坐标原点,若这个椭圆上存在点P,使得OP⊥AP。求该椭圆的离心率e的取值范围。
与x轴的正向相交于点A,O为坐标原点,若这个椭圆上存在点P,使得OP⊥AP。求该椭圆的离心率e的取值范围。

解:设椭圆 上的点P的坐标是(
上的点P的坐标是( )(α≠0且α≠π),A(a,0)。
)(α≠0且α≠π),A(a,0)。
则 。而OP⊥AP,
。而OP⊥AP,
于是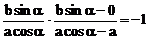 ,整理得
,整理得
解得 (舍去),或
(舍去),或 。
。
因为 ,所以
,所以 。可转化为
。可转化为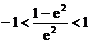 ,解得
,解得 ,于是
,于是 。故离心率e的取值范围是
。故离心率e的取值范围是 。
。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
椭圆的参数方程及其应用 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
椭圆的参数方程及其应用 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
张玲 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
例3 设点P(x,y)在椭圆 ,试求点P到直线
,试求点P到直线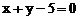 的距离d的最大值和最小值。
的距离d的最大值和最小值。
解:点P(x,y)在椭圆 上,设点P(
上,设点P( )(α是参数且
)(α是参数且 ),
),
则 。
。
当 时,距离d有最小值0,此时椭圆
时,距离d有最小值0,此时椭圆 与直线
与直线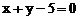 相切;当
相切;当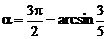 时,距离d有最大值2。
时,距离d有最大值2。
例2 已知点A在椭圆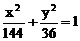 上运动,点B(0,9)、点M在线段AB上,且
上运动,点B(0,9)、点M在线段AB上,且 ,试求动点M的轨迹方程。
,试求动点M的轨迹方程。
解:由题意知B(0,9),设A( ),并且设M(x,y)。
),并且设M(x,y)。
则
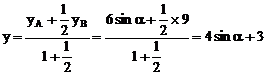 ,
,
动点M的轨迹的参数方程是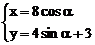 (α是参数),
(α是参数),
消去参数得 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com