
例2. 在△ABC中,若 ,试判断△ABC的形状。
,试判断△ABC的形状。
错解:由正弦定理,得
即
 。
。
∴2A=2B,即A=B。故△ABC是等腰三角形。
辨析:由 ,得2A=2B。这是三角变换中常见的错误,原因是不熟悉三角函数的性质,三角变换生疏。
,得2A=2B。这是三角变换中常见的错误,原因是不熟悉三角函数的性质,三角变换生疏。
正解:同上得 ,∴2A=
,∴2A=
或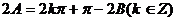 。
。
∵ 或
或 。
。
故△ABC为等腰三角形或直角三角形。
例1. 在不等边△ABC中,a为最大边,如果 ,求A的取值范围。
,求A的取值范围。
错解:∵ 。则
。则
 ,由于cosA在(0°,180°)上为减函数
,由于cosA在(0°,180°)上为减函数
且
又∵A为△ABC的内角,∴0°<A<90°。
辨析:错因是审题不细,已知条件弱用。题设是 为最大边,而错解中只把a看做是三角形的普通一条边,造成解题错误。
为最大边,而错解中只把a看做是三角形的普通一条边,造成解题错误。
正解:由上面的解法,可得A<90°。
又∵a为最大边,∴A>60°。因此得A的取值范围是(60°,90°)。
例5. 函数 时单调递减,求a的取值范围。
时单调递减,求a的取值范围。
错解:∵函数 时单调递减,
时单调递减,
∴-a=1,即a=-1。
剖析:错把函数在 时单调递减理解为函数单调递减区间是(-
时单调递减理解为函数单调递减区间是(- ,1]。事实上,当-a≥1时,函数
,1]。事实上,当-a≥1时,函数 在(1,-a]上也递减。“函数在某一区间单调”与“函数的单调区间”不要混淆。
在(1,-a]上也递减。“函数在某一区间单调”与“函数的单调区间”不要混淆。
正确解法:函数的对称轴为x=-a,因为函数在 时单调递减,故-a≥1,即a≤-1。
时单调递减,故-a≥1,即a≤-1。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
解函数的单词性时需注意的几个概念 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
解函数的单词性时需注意的几个概念 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
蔡卫琴 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
例3. 函数 的单调递增区间是( )
的单调递增区间是( )
A. 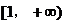 B.
(3,+
B.
(3,+ ) C.
(-
) C.
(- ,1] D.
(-
,1] D.
(- ,-1)
,-1)
错解:∵令 时,t为增函数,而y=lgt在
时,t为增函数,而y=lgt在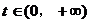 上是增函数,
上是增函数,
∴函数 的单调增区间是[1,+
的单调增区间是[1,+ )。故选A。
)。故选A。
剖析:此题除注意两个函数的单调性外,函数的定义域也不要忘记。
正确解法:此函数的定义域为(- ,-1)
,-1) 。
。
令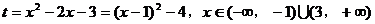
∵y=lgt在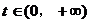 上是增函数,
上是增函数,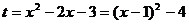 ,而
,而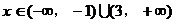 的单调增区间为(3,+
的单调增区间为(3,+ ),
),
∴选B。
例4. 已知函数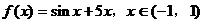 ,如果
,如果 ,则实数a的取值范围是__________。
,则实数a的取值范围是__________。
错解:由题意知f(x)是奇函数且在(-1,1)上单调递增,又由 ,得
,得 ,因此,
,因此,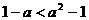 ,即
,即 或
或 。
。
剖析:忽略了复合函数的定义域,从而导致解题错误。
正确解法:由题意知f(x)是奇函数且在(-1,1)上单调递增,又由 ,得
,得
则 ,解得
,解得 。
。
例2. 若 ,且tanα<cotβ,则有( )
,且tanα<cotβ,则有( )
A.  B.
B.

C.  D.
D.
错解:因为 ,所以
,所以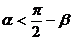 ,故选B。
,故选B。
剖析:∵
∴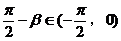 。显然,
。显然, 不在同一单调区间,故此时不能使用函数的单调性。
不在同一单调区间,故此时不能使用函数的单调性。
正确解法:∵
∴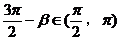 ,由题意知,
,由题意知, ,又
,又 在
在 上单调递增,故选C。
上单调递增,故选C。
例1. 证明函数 在R上是减函数。
在R上是减函数。
解:任取 ,且
,且 ,则
,则


∵
∴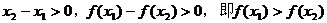
∴函数 在R上是减函数。
在R上是减函数。
提示:有的同学证明时,没有说明 ,就直接说
,就直接说 ,这个过程不能省。
,这个过程不能省。
例3. 如图4,已知球O的半径为1,A、B、C三点都在球面上,且每两点间的球面距离为 ,则球心O到平面ABC的距离为( )
,则球心O到平面ABC的距离为( )
A. 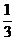 B.
B.
 C.
C.
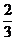 D.
D.


图4
分析:紧紧抓住球心O,由于A、B、C每两点间的球面距离为 ,因此,球心角
,因此,球心角
而OA=OB=OC=1
即O-ABC是正三棱锥
 ,
,
由
得
 ,故选B
,故选B
练习题:设地球的半径为R,若甲地位于北纬45°东经120°,乙地位于南纬75°东经120°,则甲、乙两地的球面距离为( )
A.  B.
B.
 C.
C.
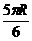 D.
D.

例2. 如图3,已知正三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC、△PEF都是正三角形,
(1)证明 平面PAB
平面PAB
(2)求二面角P-AB-C的平面角的余弦值。
(3)若点P、A、B、C在一个表面积为 的球面上,求△ABC的边长。
的球面上,求△ABC的边长。
分析:(1)利用 ,
,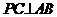 ,即可证明结论。
,即可证明结论。
(2) 是二面角P-AB-C的平面角,
是二面角P-AB-C的平面角,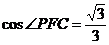
(3)由(1)(2)可证P-ABC是正三棱锥, 。如图3,把它的高PK延长交球面于另一点D,则PD是球的直径。
。如图3,把它的高PK延长交球面于另一点D,则PD是球的直径。

图3
设PA=x,球的半径为R,则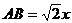 ,
, ,
,
在 中,由
中,由 ,得
,得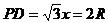

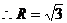 得x=2
得x=2
△ABC的边长为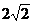
例1. 将半径都为1的四个球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为( )
A.  B.
B.

C.  D.
D.
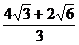
分析:设正四面体为A1-B1C1D1,它的高有最小值时,四球两两外切,并且同时内切于正四面体,两球外切时,球心连线通过切点,球心距等于两球半径之和。四球心连线构成的正四面体A-BCD(如图1)与正四面体A1-B1C1D1相似,过高AH及棱AB作的一个截面(如图2),包含其主要元素。

图1

图2
由正四面体A-BCD的棱长AB=2,求得
利用 ,得A1A=3AF1=3,而HH1=1
,得A1A=3AF1=3,而HH1=1
∴正四面体A1-B1C1D1的高A1H1的最小值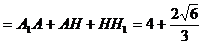
故选C
点评:解决多球相切的问题,常用的方法有两种:①连球心,转化为多面体问题;②找截面,化为平面几何问题。
2. 求角、求距离
如果要想解决线面角、二面角以及距离问题就要增加平面法向量的知识。
定义:如果n⊥α,那么向量n就叫平面α的法向量。
求解方法:
(1)异面直线所成的角α,利用它们所对应的向量转化为向量的夹角θ问题,但 ,
, ,所以
,所以
(2)直线与平面所成的角,利用直线的方向向量与平面的法向量夹角的余角(或补角的余角)。如图2: 。
。
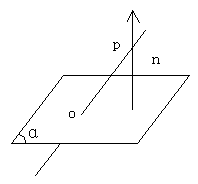
图2
(3)求二面角,转化为两平面法向量的夹角或夹角的补角,显见上述求法都避开了找角的繁琐,直接计算就可以了。
求点面距离,转化为此点与面内一点连线对应向量在法向量上投影的绝对值。
例3. (2005年高考题)如图3,已知长方体ABCD-A1B1C1D1中,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点。
(1)求异面直线AE与BF所成的角。
(2)求平面BDF与平面AA1B所成二面角(锐角)的大小。
(3)求点A到平面BDF的距离。

图3
解:在长方体ABCD-A1B1C1D1中,以AB所在直线为x轴,AD所在直线为y轴,AA1所在直线为z轴,建立空间直角坐标系如图3,
所以A(0,0,0),B(2,0,0),F(1,0,1),因为直线BD与平面AA1B1B所成的角为30°,所以∠DBA=30°
又AB=2,AE⊥BD,所以AE=1,AD= ,因为E(
,因为E(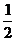 ,
, ,0),D(0,
,0),D(0, ,0)
,0)
(1)因为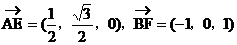
所以
即异面直线AE、BF所成的角为
(2)易知平面AA1B的一个法向量m=(0,1,0),设n=(x,y,z)是平面BDF的一个法向量,
由
所以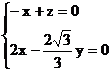
取
所以
(3)点A到平面BDF的距离即 在平面BDF的法向量n上的投影的绝对值。
在平面BDF的法向量n上的投影的绝对值。
所以
例4. 如图4,已知正四棱锥R-ABCD的底面边长为4,高为6,点P是高的中点,点Q是侧面RBC的重心。求直线PQ与底面ABCD所成的角。

图4
解:以O为原点,以OR所在直线为z轴,以过O与AB垂直的直线为x轴,与AB平行的直线为y轴建立空间直角坐标系。
因为底面边长为6,高为4,所以B(2,2,0),C(-2,2,0),R(0,0,6),所以Q(0, ,2),P(0,0,3),
,2),P(0,0,3), (0,
(0, ,-1),面ABCD的一个法向量为n=(0,0,1),设PQ与底面ABCD所成的角为α,则
,-1),面ABCD的一个法向量为n=(0,0,1),设PQ与底面ABCD所成的角为α,则 。
。
空间向量在立体几何中的应用体现了数形结合的思想,培养了学生使用向量代数方法解决立体几何问题的能力。目的是将空间元素的位置关系转化为数量关系,将形式逻辑证明转化为数值计算,用数的规范性代替形的直观性、可操作性强,解决问题的方法具有普遍性,大大降低了立体几何对空间想象能力要求的难度。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
浅谈向量在几何中的应用 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
浅谈向量在几何中的应用 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
许咏梅 |
一校 |
郭敏 |
二校 |
|
审核 |
|
||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com