
3.已知不等式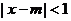 成立的一个充分非必要条件是
成立的一个充分非必要条件是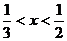 ,则实数
,则实数 的取值范围是 ( )
的取值范围是 ( )
A.  B.
B.  C.
C. 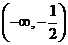 D.
D. 
2.设 是实数,则“
是实数,则“ ”是“
”是“ ”的
( )
”的
( )
A.充分而不必要条件 B.必要而不充分条件C. 充要条件D. 既不充分也不必要条件
既不充分也不必要条件
1.已知 ,
,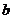 都是实数,则“
都是实数,则“ ”是“
”是“ ”的( )
”的( )
A.充分不必 要条件
B.必要不充分条件
要条件
B.必要不充分条件
C.充分必 要条件
D.既不充分又不
要条件
D.既不充分又不 必要条件
必要条件
6. 忽视特殊化法的片面性
例6. 设集合A,B是两个非空集合,我们规定 ,根据上述规定,则
,根据上述规定,则 ( )
( )
A. M B.
N C.
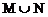 D.
D.
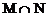
错解:特殊化法。取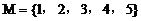 ,
,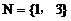
则

故选A
分析:这种特殊化法对原题作了 的前提假定,缩小了原题中B集合的取值范围,如
的前提假定,缩小了原题中B集合的取值范围,如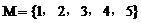 ,
,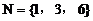
则

而是
实际上,对规定 有两种理解:
有两种理解:
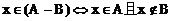 ,或
,或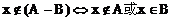
所以
而
故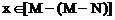

所以
选D
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
集合中的易错之处 |
||||||||||||
|
分类索引号 |
G.622.475 |
分类索引描述 |
统考试题与题解 |
||||||||||
|
主题词 |
集合中的易错之处 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩秋荣 |
一校 |
陈丽娜 |
二校 |
|
审核 |
|
||||||
5. 忽视语言转换的等价性
例5. 设全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A.  B.
B.

C. (2,3) D.

分析:容易错选A,原因是将集合M看作直线 上的点的集合,实际上应除去点(2,3)。集合N是坐标平面内不在直线y=x+1上的点的集合,所以
上的点的集合,实际上应除去点(2,3)。集合N是坐标平面内不在直线y=x+1上的点的集合,所以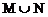 是坐标平面上除去(2,3)以外的点构成的集合,它的补集
是坐标平面上除去(2,3)以外的点构成的集合,它的补集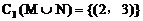 ,应选B。
,应选B。
4. 忽视补集的相对性
例4. 已知全集 ,集合
,集合 ,则
,则 _________;若全集为
_________;若全集为 ,则
,则 __________。
__________。
分析:补集是相对于全集而言的,当全集发生变化时,补集也随之变化。显然,在全集 的条件下,
的条件下,
在全集为I=R的条件之下,
3. 忽视空集
例3. 若集合 ,
, ,且
,且 ,求实数m的值。
,求实数m的值。
错解:因为 ,所以
,所以 或
或
即 或
或
分析:上面的解法中漏掉了 即
即 的情形,因为空集是任何非空集合的真子集,所以
的情形,因为空集是任何非空集合的真子集,所以 或
或 或m=0。
或m=0。
2. 忽视元素的互异性
例2. 已知集合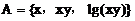 ,
, ,若A=B,求实数x,y的值。
,若A=B,求实数x,y的值。
错解:因为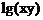 有意义,所以xy>0,从而
有意义,所以xy>0,从而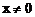 ,故xy=1
,故xy=1
又由A=B得 或
或
所以 或
或
分析:由于同一集合中的元素不同(互异性),而以上解法中,当 时,
时, ,
, 分别使集合A,B中出现了相同元素,故应舍去,所以只能取
分别使集合A,B中出现了相同元素,故应舍去,所以只能取 。
。
1. 忽视代表元素的属性
例1. 集合 ,
, ,则
,则 ( )
( )
A.  B.
B.

C.  D.
D.

错解:由
解得 或
或
选B
分析:注意到两个集合中的元素y都是各自函数的函数值,因此,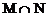 应是
应是 和
和 这两个函数的值域的交集,而不是它们的交点。由于
这两个函数的值域的交集,而不是它们的交点。由于 ,
, ,所以
,所以 ,选C。
,选C。
二次函数是含参数的函数,而定义域区间也是变化的,我们称这种情况是“动二次函数在动区间上的最值”。
例7. 已知 ,且当
,且当 时,
时, 的最小值为4,求参数a的值。
的最小值为4,求参数a的值。
解:将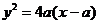 代入S中,得
代入S中,得

则S是x的二次函数,其定义域为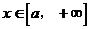 ,对称轴方程为
,对称轴方程为 ,顶点坐标为
,顶点坐标为 ,图象开口向上。
,图象开口向上。
若 ,即
,即
则当 时,
时,
此时, ,或
,或
若 ,即
,即
则当 时,
时,
此时, ,或
,或 (因
(因 舍去)
舍去)
综上讨论,参变数a的取值为 ,或
,或 ,或
,或
例8. 已知 ,且当
,且当 时,
时,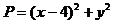 的最小值为1,求参变数a的值。
的最小值为1,求参变数a的值。
解:将 代入P中,得
代入P中,得

则P是x的二次函数,其定义域为 ,对称轴方程为
,对称轴方程为 ,顶点坐标为
,顶点坐标为 ,图象开口向上。
,图象开口向上。
若 ,即
,即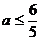
则当 时,
时,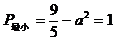
此时,
若 ,即
,即
则当 时,
时,
此时, ,或
,或 (因
(因 舍去)
舍去)
综上讨论,
解后反思:例7中,二次函数的对称轴是变化的;例8中,二次函数的对称轴是固定的。
另外,若函数图象的开口方向、对称轴均不确定,且动区间所含参数与确定函数的参数一致,可采用先斩后奏的方法。二次函数在闭区间上的最值只可能在区间端点、顶点处取得,不妨令之为最值,验证参数的资格,进行取舍。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
闭区间上二次函数的最值 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
闭区间上二次函数的最值 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
韩素果 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com