22．(本小题满分15分)

已知函数，.

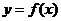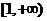(Ⅰ)如果函数在上是单调增函数，求的取值范围；

(Ⅱ)是否存在实数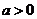，使得方程在区间内有且只有两个不相等的实数根？若存在，请求出的取值范围；若不存在，请说明理由．

21．(本小题满分15分)

椭圆C的中心在坐标原点O，焦点在轴上，离心率为，以短轴的一个端点与两焦点为顶点的三角形的面积为．高@考@资@源@网

(1)求椭圆C的方程；

(2)若过点存在直线与椭圆C交于相异两点A，B，满足：且，求常数的值和实数的取值范围．

解：(1)设椭圆的方程为：，

由题意知，，且，

解得：，．

故椭圆C的方程为：．

(2)由得，，

∴，

∴，．

当直线与轴不垂直时，设直线的方程为：，

且与椭圆C的交点为，，

由得：，

∴，

，，

由得，

∴，，

消去得：，

即，．

当时，上式不成立，，∴，高@考@资@源@网

代入，即，得恒成立，

即，解得，

∴或．

当直线与轴垂直时，的方程为：得．

综上所述：的取值范围为．

20．解：(1)设运动员得4分的事件为A，则　　　　　　　　　 4分

　 (2)设运动员得分数的可能取值为0，1，2，3，4　 的分布列为

	0	1	2	3	4
P

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

数学期望

　　　　　　　　　　　　　　　　　　　　　 14分

20．(本小题满分14分)

　　　 射击运动员在双向飞碟射击比赛中，每轮比赛连续发射两枪，击中两个飞靶得2分，击中一个得1分，未击中得0分。某运动员在每轮比赛时，第一枪命中率为，第二枪命中率为，该运动员只进行两轮比赛。

　 (1)求该运动员得4分的概率；

　 (2)若该运动员所得分数为的分布列及数学期望。

19．(本大题共14分)

如图所示，ABCD为矩形，平面ABE，，F为CE上的点，且平面ACE.

(1)求证：平面BFD；

(2)求证：平面BCE；

(3)求平面BDF与平面ABE所成的二面角的正弦值.

(1)证明：连AC交BD于G，由题意可得G是AC的中点，可得F是EC的中点.

在中，，平面BFD. ………5分

(2) 平面ABE，，

平面ABE，则，

又平面ACE，则，

平面BCE. ……………………………………10分

(3)可以以AB中点O为原点，OE为x轴，OB为y轴，

OG为z轴，建立空间直角坐标系.通过计算法向量，

计算，所以平面BDF与平面ABE所成的二面角的正弦值为.

……………………………………………………………………………………………15分

18．(本小题满分14分)

在中，角的对边分别为，，的面积为.

(Ⅰ)求，的值；

(Ⅱ)求的值.　　

解：(Ⅰ)由已知，，，

因为　 　，　　　　 　　　　　　　　　　

即　　 　，　　　　　　　　　　　　　　　　　　　　　　 ………………..1分

解得　 　　　 .　　　　　　　　　　　　　　　　　 ………………..3分

由余弦定理可得:,　　　　　　　　　　 ………………..5分

所以　 .　　　　　　　　　　　　　　　　　　　　 ………………..7分

(Ⅱ)由(Ⅰ)有,　　　　　　　　　　　　　　　　 ………………..9分

由于A是三角形的内角，

易知　 ,　　　　　　　　　　　　　　　　　　　 ………………..10分

　　　　 所以　 　　　　　　 ………………..11分

　　　　　　　　　　　 　.　　　　　　　　　　　　　 　………………..13分

17．　　 ①③④_　　　　　

15．　　　 　　　　　　　　　　　　　　16．　 　　　　　　　　

13． 1, 　　　　14．　　 　　　　　　

11．　　　 2　　 　　　　　　　　　　　　12．　　 294