
9.对于函数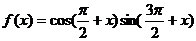 ,给出下列四个结论:①函数
,给出下列四个结论:①函数 的最小正周期为
的最小正周期为 ;②若
;②若 ③
③ 的图象关于直线
的图象关于直线 对称;④
对称;④ 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )
A.2 B.4 C.1 D.3
8.如果执行右侧的程序框图,那么输出的S的值为( )
A.2450 B.2550
C.2500 D.2652
6.若不等式组 表示的平面区域是一个三角形,则实数s的取值范围是( )
表示的平面区域是一个三角形,则实数s的取值范围是( )
A. B.
B.
C.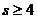 D.
D.
 7.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为 ( )
7.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为 ( )
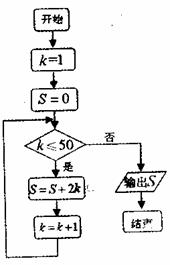
A.1 B.
C.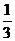 D.
D.
5.设集合 ,命题
,命题 若
若 为真命题,
为真命题, 为假命题,则a的取值范围是 ( )
为假命题,则a的取值范围是 ( )
A. B.
B.
C. D.
D.
4.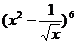 的二项展开式中
的二项展开式中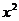 的系数为 ( )
的系数为 ( )
A.15 B.-15 C.30 D.-30
3.已知函数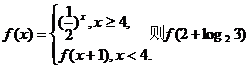 的值为 ( )
的值为 ( )
A.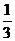 B.
B. C.
C. D.
D.
1.复数 (i是虚数单位)的虚部为 ( )
(i是虚数单位)的虚部为 ( )
A.-1 B.0 C.1 D.2
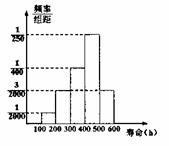 2.对某种电子元件进行寿命跟踪调查,所得样本频率分布直
2.对某种电子元件进行寿命跟踪调查,所得样本频率分布直
方图如右图,由图可知:一批电子元件中,寿命在100~300
小时的电子元件的数量与寿命在300~600小时的电子元件的
数量的比大约是 ( )
A. B.
B.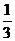
C. D.
D.
22.(本题满分14分)
设曲线
(1)若函数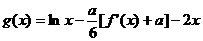 存在单调递减区间,求a的取值范围
存在单调递减区间,求a的取值范围
(2)若过曲线C外的点A(1,0)作曲线C的切线恰有三条,求a,b满足的关系式。
21.(本题满分12分)
如图,斜率为1的直线 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)

20.(本小题满分12分)
 如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点。
如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点。
(1)求证:BC//平面EFG;
(2)求三棱锥E-AFG的体积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com