
7.将函数 的图像按向量
的图像按向量 平移,则平移后的函数图像的解析式为
平移,则平移后的函数图像的解析式为
(A)  (B)
(B)

( C)  (D)
(D) 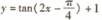
6. 在等差数列 中,若
中,若 ,则它的前10项和
,则它的前10项和
(A)70 (B)80 (C)90 (D)IOO
5.某篮球运动员在三分线投篮的命准率为 ,他投篮5次,恰好投准3次的概率为
,他投篮5次,恰好投准3次的概率为
(A)  (B)
(B) 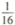 ( C)
( C) 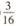 (D)
(D) 
4.下列四个数中,最大的一个是
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
3.在△ABC中,若 ,则△ABC的形状为
,则△ABC的形状为
(A)直角三角形 (B)等边三角形 (c)等腰三角形 (D)等腰直角三角形
2.计算: =
=
(A)I +3i (B)3+3i (C)1-3i (D)3 -3i
1.已知集合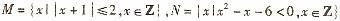 .则
.则 =
=
(A) 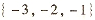 (B)
(B)  (C)
(C) 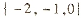 (D)
(D) 
2.(万有引力定律+单摆+圆周运动)有人设想在地球赤道上垂直于地球表面竖起一根刚性的长杆,杆子的长度是地球半径的若干倍。长杆随地球一起自转。在长杆上距地面高度为h=R(R为地球半径)处, 悬挂一个摆长为L,质量为m的单摆(L远远小于R)。设地球半径R、地球表面的重力加速度g地球的自转周期T0均为已知,
(1)悬挂单摆处随地球自转的向心加速度多大?
(2)该单摆的振动周期为多少?
(3)单摆悬挂于长杆上距地球表面的高度H为多高处,单摆就无法振动?
解:



1.(平抛运动+运动的分解+功能关系或牛顿运动定律)倾斜雪道的长为25 m,顶端高为15 m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示。一滑雪运动员在倾斜雪道的顶端以水平速度v0=8 m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起。除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略。设滑雪板与雪道的动摩擦因数μ=0.2,求运动员在水平雪道上滑行的距离(取g=10 m/s2)
解:如图选坐标,斜面的方程为:

 (1分)
(1分)
运动员飞出后做平抛运动
 (1分)
(1分)
 (1分)
(1分)
联立三式,得飞行时间: t=1.2 s (1分)
落点的x坐标:x1=v0t=9.6 m
落点离斜面顶端的距离: (1分)
(1分)
落点距地面的高度: (1分)
(1分)
接触斜面前的x分速度:
y分速度: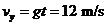
沿斜面的速度大小为: (2分)
(2分)
设运动员在水平雪道上运动的距离为s2,由功能关系得:
 (2分)
(2分)
解得:s2=74.8 m (2分)
(用牛顿运动定律解得s2=74.8 m,同样给分)
3. 用长L=1.6m的细绳,一端系着质量M=1kg的木块,另一端挂在固定点上。现有一颗质量=20g的子弹以v1=500m/s的水平速度向木块中心射击,结果子弹穿出木块后以v2=100m/s的速度前进。问木块能运动到多高?(取g=10m/s2,空气阻力不计)
[错解]在水平方向动量守恒,有
mv1=Mv+mv2 (1)
式①中v为木块被子弹击中后的速度。木块被子弹击中后便以速度v开始摆动。由于绳子对木块的拉力跟木块的位移垂直,对木块不做功,所以木块的机械能守恒,即

h为木块所摆动的高度。解①,②联立方程组得到
v=8(v/s)
h=3.2(m)
[错解原因]这个解法是错误的。h=3.2m,就是木块摆动到了B点。如图4-3所示。则它在B点时的速度vB。应满足方程
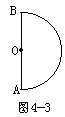

这时木块的重力提供了木块在B点做圆周运动所需要的向心力。解

如果vB<4 m/s,则木块不能升到B点,在到达B点之前的某一位置以某一速度开始做斜向上抛运动。而木块在B点时的速度vB=4m/s,是不符合机械能守恒定律的,木块在 B点时的能量为(选A点为零势能点)

两者不相等。可见木块升不到B点,一定是h<3.2 m。
实际上,在木块向上运动的过程中,速度逐渐减小。当木块运动到某一临界位置C时,如图4 -4所示,木块所受的重力在绳子方向的分力恰好等于木块做圆周运动所需要的向心力。此时绳子的拉力为零,绳子便开始松弛了。木块就从这个位置开始,以此刻所具有的速度vc作斜上抛运动。木块所能到达的高度就是C点的高度和从C点开始的斜上抛运动的最大高度之和。
[分析解答] 如上分析,从式①求得vA=v=8m/s。木块在临界位置C时的速度为vc,高度为
h′=l(1+cosθ)
如图所示,根据机船能守恒定律有


木块从C点开始以速度vc做斜上抛运动所能达到的最大高度h″为

[评析] 物体能否做圆运动,不是我们想象它怎样就怎样这里有一个需要的向心力和提供向心力能否吻合的问题,当需要能从实际提供中找到时,就可以做圆运动。所谓需要就是符合牛顿第二定律F向=ma向的力,而提供则是实际中的力若两者不相等,则物体将做向心运动或者离心运动。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com