
近年来,上海市对部分县区功能进行了重新定位,据此回答7-8题。
7.宝山区从“钢铁宝山”转变为“精钢宝山”,其原因不可能是
A.集约型发展的需要 B.循环经济的需要
C.产业升级的需要 D.美化环境的需要
8.上海市对崇明岛的开发进行了综合规划,你认为崇明区(岛)的功能最应该界定为
A.“生态崇明” B.“商业崇明” C.“渔业崇明” D.“知识崇明”
2009 年11月份,我国过早进入了冬季,并在全国出现大范围降雪天气,致使天然气使用量大大增加,部分城市出现天然气供给不足的状况。一月之间,国内天然气批发价格暴涨,平均涨幅超过 20%。据此回答 5-6题。
5.造成此次“天然气荒”的原因,与下列说法无关的是
A.极端天气导致的需求量猛增 B.天然气供需矛盾突出
C.天然气价格远远低于石油价格 D.国内天然气资源的生产地与需求地不匹配
6.下列缓解天然气荒的措施正确的是
①建立和完善天然气储备机制 ②多渠道地扩大天然气进口量
③持续提高天然气的市场价格 ④提高煤炭消费量,缓解天然气供应的不足
A. ①② B. ②③ C. ③④ D. ②④
读我国某时近地面气压分布状况图,回答3-4题。

3.此时,图中A点的风向是
A.偏北风 B.西南风 C.南风 D.不确定
4.未来几天内河套地区天气状况可能是
①气压降低 ②大风 ③气温升高 ④降温
A.①② B.②③ C.①③ D.②④
 读“世界局部地区图”,当图中PQ线为昏线且与极圈相切时,回答1-2题。
读“世界局部地区图”,当图中PQ线为昏线且与极圈相切时,回答1-2题。
1.此时,里斯本与马赛相比
A.正午太阳高度小 B.白昼时间长
C.自转线速度小 D.自转角速度大
2.A、B两地均盛产葡萄。两地相比,A地的优势是
A.交通便捷 B.市场广阔 C.鲜果上市早 D.技术条件好
22.(本题满分14分)
已知二次函数 ,其导函数
,其导函数 的图象如图,
的图象如图,


(1)求函数 处的切线斜率;
处的切线斜率;
(2)若函数 上是单调函数,求实数
上是单调函数,求实数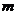 的取值范围;
的取值范围;
(3)若 的图像总在函数
的图像总在函数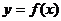 图象的上方,求
图象的上方,求 的取值范围.
的取值范围.
21.(本小题满分12分)
已知圆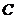 的圆心为
的圆心为 ,半径为
,半径为 ,圆
,圆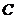 与椭圆
与椭圆 :
: 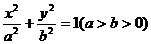 有一个公共点
有一个公共点 (3,1),
(3,1), 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆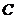 的标准方程;
的标准方程;
(2)若点P的坐标为(4,4),试探究斜率为k的直线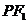 与圆
与圆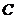 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆 和直线
和直线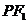 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
20.(本小题满分12分)
某校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;
[80,90),12;[90,100),4.
(1)请把给出的样本频率分布表中的空格都填上;
(2)估计成绩在85分以上学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100)中选两位同学,共同帮助[40,50)中的某一位同学.已知甲同学的成绩为42分, 乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表
|
分组 |
频数 |
频率 |
|
[40,50) |
2 |
0.04 |
|
[50,60) |
3 |
0.06 |
|
[60,70) |
14 |
0.28 |
|
[70,80) |
15 |
0.30 |
|
[80,90) |
|
|
|
[90,100) |
4 |
0.08 |
|
合计 |
|
|
19.(本题满分12分)
已知点(1,2)是函数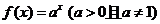 的图象上
的图象上
一点,数列 的前
的前 项和
项和 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
18.(本小题满分12分)
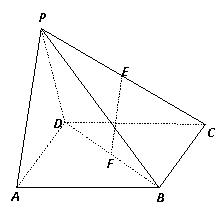 如图,在四棱锥P-ABCD中,底面ABCD是边长为
如图,在四棱锥P-ABCD中,底面ABCD是边长为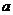 的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
17.(本小题满分12分)
已知x∈R, >0,u=(
>0,u=(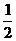 ,sin(
,sin(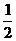
 x+
x+ )),v=(cos
)),v=(cos x,
x, sin
sin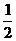
 x),函数f(x)=1+u·v的最小正周期为
x),函数f(x)=1+u·v的最小正周期为 .
.
(1)求 的值;
的值;
(2)求函数f(x)在区间[0,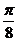 ]上的值域.
]上的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com