
五种常见函数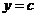 、
、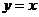 、
、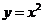 、
、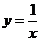 、
、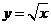 的导数公式及应用
的导数公式及应用
|
函数 |
导数 |
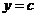 |
 |
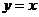 |
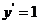 |
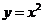 |
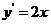 |
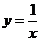 |
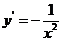 |
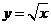 |
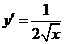 |
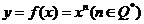 |
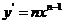 |
|
函数 |
导数 |
 |
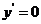 |
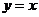 |
 |
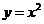 |
 |
 |
 |
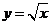 |
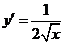 |
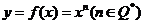 |
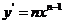 |
2.课本P13探究2
1.课本P13探究1
5.函数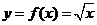 的导数
的导数
因为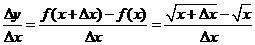
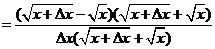
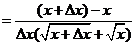
所以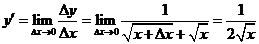
|
函数 |
导数 |
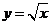 |
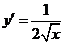 |
(2)推广:若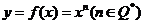 ,则
,则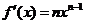
4.函数 的导数
的导数
因为
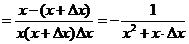
所以
|
函数 |
导数 |
 |
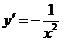 |
3.函数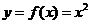 的导数
的导数
因为
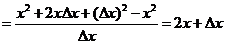
所以
|
函数 |
导数 |
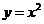 |
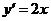 |
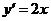 表示函数
表示函数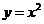 图像(图3.2-3)上点
图像(图3.2-3)上点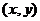 处的切线的斜率都为
处的切线的斜率都为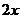 ,说明随着
,说明随着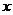 的变化,切线的斜率也在变化.另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当
的变化,切线的斜率也在变化.另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当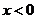 时,随着
时,随着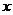 的增加,函数
的增加,函数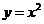 减少得越来越慢;当
减少得越来越慢;当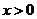 时,随着
时,随着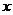 的增加,函数
的增加,函数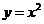 增加得越来越快.若
增加得越来越快.若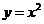 表示路程关于时间的函数,则
表示路程关于时间的函数,则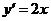 可以解释为某物体做变速运动,它在时刻
可以解释为某物体做变速运动,它在时刻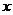 的瞬时速度为
的瞬时速度为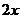 .
.
2.函数 的导数
的导数
因为
所以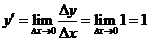
|
函数 |
导数 |
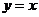 |
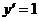 |
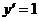 表示函数
表示函数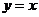 图像(图3.2-2)上每一点处的切线的斜率都为1.若
图像(图3.2-2)上每一点处的切线的斜率都为1.若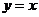 表示路程关于时间的函数,则
表示路程关于时间的函数,则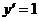 可以解释为某物体做瞬时速度为1的匀速运动.
可以解释为某物体做瞬时速度为1的匀速运动.
1.函数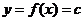 的导数
的导数
根据导数定义,因为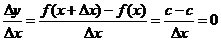
所以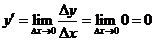
|
函数 |
导数 |
 |
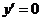 |
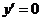 表示函数
表示函数 图像(图3.2-1)上每一点处的切线的斜率都为0.若
图像(图3.2-1)上每一点处的切线的斜率都为0.若 表示路程关于时间的函数,则
表示路程关于时间的函数,则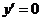 可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.
可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.
我们知道,导数的几何意义是曲线在某一点处的切线斜率,物理意义是运动物体在某一时刻的瞬时速度.那么,对于函数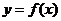 ,如何求它的导数呢?
,如何求它的导数呢?
由导数定义本身,给出了求导数的最基本的方法,但由于导数是用极限来定义的,所以求导数总是归结到求极限这在运算上很麻烦,有时甚至很困难,为了能够较快地求出某些函数的导数,这一单元我们将研究比较简捷的求导数的方法,下面我们求几个常用的函数的导数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com