
例1(课本例4)求下列函数的导数:
(1) ;(2)
;(2)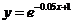 ;
;
(3) (其中
(其中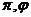 均为常数).
均为常数).
解:(1)函数 可以看作函数
可以看作函数 和
和 的复合函数。根据复合函数求导法则有
的复合函数。根据复合函数求导法则有
 =
= 。
。
(2)函数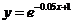 可以看作函数
可以看作函数 和
和 的复合函数。根据复合函数求导法则有
的复合函数。根据复合函数求导法则有
 =
=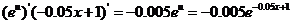 。
。
(3)函数 可以看作函数
可以看作函数 和
和 的复合函数。根据复合函数求导法则有
的复合函数。根据复合函数求导法则有
 =
=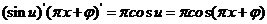 。
。
例2求 的导数.
的导数.
解:

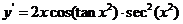
[点评]
求复合函数的导数,关键在于搞清楚复合函数的结构,明确复合次数,由外层向内层逐层求导,直到关于自变量求导,同时应注意不能遗漏求导环节并及时化简计算结果.
例3求 的导数.
的导数.
解: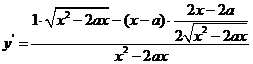
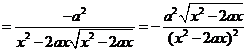 ,
,
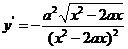
[点评]本题练习商的导数和复合函数的导数.求导数后要予以化简整理.
例4求y =sin4x +cos 4x的导数.
[解法一]y =sin
4x +cos 4x=(sin2x +cos2x)2-2sin2cos2x=1- sin22 x
sin22 x
=1- (1-cos
4 x)=
(1-cos
4 x)= +
+ cos 4 x.y′=-sin 4 x.
cos 4 x.y′=-sin 4 x.
[解法二]y′=(sin 4 x)′+(cos 4 x)′=4 sin 3 x(sin x)′+4 cos 3x (cos x)′
=4 sin 3 x cos x +4 cos 3 x (-sin x)=4 sin x cos x (sin 2 x -cos 2 x)
=-2 sin 2 x cos 2 x=-sin 4 x
[点评]
解法一是先化简变形,简化求导数运算,要注意变形准确.解法二是利用复合函数求导数,应注意不漏步.
例5曲线y =x(x +1)(2-x)有两条平行于直线y =x的切线,求此二切线之间的距离.
[解]y =-x 3 +x 2 +2 x y′=-3 x 2+2 x +2
令y′=1即3 x2-2 x -1=0,解得 x =-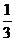 或x =1.
或x =1.
于是切点为P(1,2),Q(-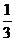 ,-
,-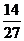 ),
),
过点P的切线方程为,y -2=x -1即 x -y +1=0.
显然两切线间的距离等于点Q 到此切线的距离,故所求距离为
 =
=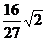 .
.
复合函数的概念 一般地,对于两个函数 和
和 ,如果通过变量
,如果通过变量 ,
, 可以表示成
可以表示成 的函数,那么称这个函数为函数
的函数,那么称这个函数为函数 和
和 的复合函数,记作
的复合函数,记作 。
。
复合函数的导数 复合函数 的导数和函数
的导数和函数 和
和 的导数间的关系为
的导数间的关系为 ,即
,即 对
对 的导数等于
的导数等于 对
对 的导数与
的导数与 对
对 的导数的乘积.
的导数的乘积.
若 ,则
,则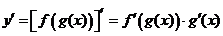
(二)导数的运算法则
|
导数运算法则 |
1. 2. 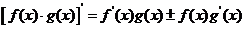 3.  |
(2)推论:
(常数与函数的积的导数,等于常数乘函数的导数)
(一)基本初等函数的导数公式表
|
函数 |
导数 |
 |
 |
 |
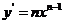 |
 |
 |
 |
 |
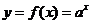 |
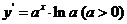 |
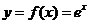 |
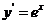 |
 |
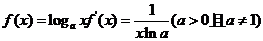 |
 |
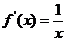 |
(1)基本初等函数的导数公式表
(2)导数的运算法则
2.已知曲线C:y =3 x 4-2 x3-9 x2+4,求曲线C上横坐标为1的点的切线方程;
(y =-12 x +8)
1.课本P92练习
例1.假设某国家在20年期间的年均通货膨胀率为 ,物价
,物价 (单位:元)与时间
(单位:元)与时间 (单位:年)有如下函数关系
(单位:年)有如下函数关系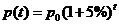 ,其中
,其中 为
为 时的物价.假定某种商品的
时的物价.假定某种商品的 ,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01)?
,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01)?
解:根据基本初等函数导数公式表,有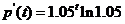
所以 (元/年)
(元/年)
因此,在第10个年头,这种商品的价格约为0.08元/年的速度上涨.
例2.根据基本初等函数的导数公式和导数运算法则,求下列函数的导数.
(1)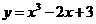
(2)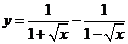 ;
;
(3)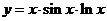 ;
;
(4)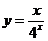 ;
;
(5) .
.
(6) ;
;
(7)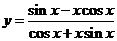
解:(1) ,
,
 。
。
(2)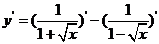





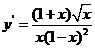
(3)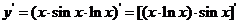
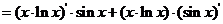
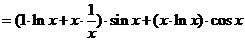
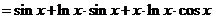
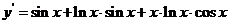
(4) ,
,
 。
。
(5)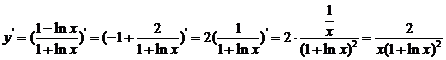

(6)
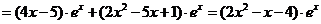 ,
,
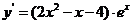 。
。
(7)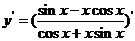



 。
。

[点评]
① 求导数是在定义域内实行的.
② 求较复杂的函数积、商的导数,必须细心、耐心.
例3日常生活中的饮水通常是经过净化的.随着水纯净度的提高,所需净化费用不断增加.已知将1吨水净化到纯净度为 时所需费用(单位:元)为
时所需费用(单位:元)为

求净化到下列纯净度时,所需净化费用的瞬时变化率:(1)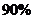 (2)
(2)
解:净化费用的瞬时变化率就是净化费用函数的导数.



(1)
因为 ,所以,纯净度为
,所以,纯净度为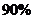 时,费用的瞬时变化率是52.84元/吨.
时,费用的瞬时变化率是52.84元/吨.
(2)
因为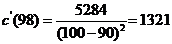 ,所以,纯净度为
,所以,纯净度为 时,费用的瞬时变化率是1321元/吨.
时,费用的瞬时变化率是1321元/吨.
函数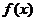 在某点处导数的大小表示函数在此点附近变化的快慢.由上述计算可知,
在某点处导数的大小表示函数在此点附近变化的快慢.由上述计算可知, .它表示纯净度为
.它表示纯净度为 左右时净化费用的瞬时变化率,大约是纯净度为
左右时净化费用的瞬时变化率,大约是纯净度为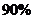 左右时净化费用的瞬时变化率的25倍.这说明,水的纯净度越高,需要的净化费用就越多,而且净化费用增加的速度也越快.
左右时净化费用的瞬时变化率的25倍.这说明,水的纯净度越高,需要的净化费用就越多,而且净化费用增加的速度也越快.
(二)导数的运算法则
|
导数运算法则 |
1. 2. 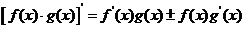 3.  |
(2)推论:
(常数与函数的积的导数,等于常数乘函数的导数)
(一)基本初等函数的导数公式表
|
函数 |
导数 |
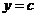 |
 |
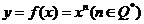 |
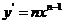 |
 |
 |
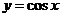 |
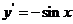 |
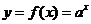 |
 |
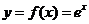 |
 |
 |
 |
 |
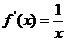 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com