
9.下列有关平面向量分解定理的四个命题中,所有正确命题的序号是 . (填写命题所对应的序号即可)
① 一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
② 一个 平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
③ 平面向量的基向量可能互相垂直;
④ 一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组 合.
合.
8.一个圆柱形容器的轴截面尺寸如右图所示,容器内有一个实心的球,球的直径恰等于圆柱的高.现用水将该容器注满,然后取出该球(假设球的密度大于水且操作过程中水量损失不计),则球取出后,容器中水面的高度为
 cm. (精确到0.1cm)
cm. (精确到0.1cm)
7. 在 的二面角内放一个半径为
的二面角内放一个半径为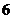 的球,使球与两个半平面各只有一个公共点(其过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB之间的球面距离为
.
的球,使球与两个半平面各只有一个公共点(其过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB之间的球面距离为
.
6.若取地球的半径为 米,球面上两点
米,球面上两点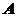 位于东经
位于东经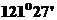 ,北纬
,北纬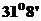 ,
, 位于东经
位于东经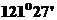 ,北纬
,北纬 ,则
,则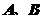 两点的球面距离为_____________千米(结果精确到1千米).
两点的球面距离为_____________千米(结果精确到1千米).
5.在长方体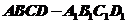 中,若
中,若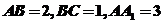 ,则
,则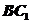 与平面
与平面 所成的角
所成的角 可用反三角函数值表示为
可用反三角函数值表示为 ____________.
____________.
4.若圆锥的侧面积为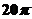 ,且母线与底面所成的角为
,且母线与底面所成的角为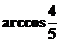 ,则该圆锥的体积为___________.
,则该圆锥的体积为___________.
3.如图,是一个无盖正方体盒子的表面展开图, 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ____________.
____________.
2. 联结球面上任意两点的线段称为球的弦,已知半径为
联结球面上任意两点的线段称为球的弦,已知半径为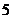 的球上有两条长分别为
的球上有两条长分别为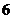 和
和 的弦,则此两弦中点距离的最大值是____________.
的弦,则此两弦中点距离的最大值是____________.
1.已知圆锥的母线长为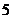
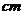 ,侧面积为
,侧面积为
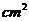 ,则此圆锥的体积为__________
,则此圆锥的体积为__________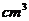 .
.
10.在底面为正方形的长方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,①矩形;②不是矩形的平行四边形;③有三个面为直角三角形, 有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.
有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.
这些几何形体是( )
A.①②④⑤ B.①②③⑤ C.①②③④ D.①③④⑤
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com